Collection of Solved Problems in Physics

Calculation of the Spectrum Width

Task number: 2213

• A picture of the situation

  

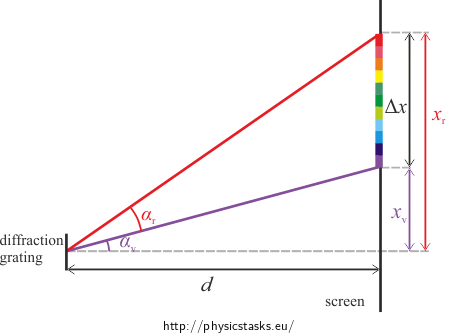
  We denoted: d the distance between the diffraction grating and the screen, x _v the distance between the first and zero order violet maxima , α_v the angle of the first order violet maximum, x_r the distance between the first and zero order red maxima, α_r is the angle of the first order red maximum and Δx the width of the spectrum on the screen in the picture.

• Hint 1

  Try to find an equation for angles α_v and α_r using the optical path difference Δl and a groove spacing b.

• Hint 1 solution

  It holds for angle α_r ithat:

  \[\sin\,α_\mathrm{r} = \, \frac{\mathrm{Δ}l_\mathrm{r}}{b},\]

  where Δl_r is a path difference and b is a groove period.

  For angle α_v similarly. Il holds that:

  \[\sin\,α_\mathrm{r} = \, \frac{\mathrm{Δ}l_\mathrm{r}}{b},\]

  where Δl_v is a path difference and b is a groove period.

  You will find the step-by-step solution in the task Deflection of the First Diffraction Maximum at a Grating.

  As we aim to calculate the maxima we set Δl = kλ where k denotes the order or the maximum, thus k = 1.

  For the wavelength λ we substitute the wavelength of red or violet light respectively.

  \[\sin\,α_r = \, \frac{λ_\mathrm{r}}{b}\quad \mathrm{a} \quad \sin\,α_v = \, \frac{λ_\mathrm{v}}{b}.\]

  We can express the angles α_r a α_v from the above equations.

• Hint 2

  Use the image above to express the spectrum width Δx using the distances x_v, x_r and angles α_f, α_č.

• Hint 2 solution

  To calculate the width of the spectrum Δx we must express it using the physical quantities we know. We can simply write the width of the spectrum on the screen Δx as the difference of distances x_v and x_r:

  \[\mathrm{Δ}x=\, x_\mathrm{č} − x_\mathrm{f}. \]

  From the image above we can express x_r as:

  \[x_\mathrm{r}=\, d\,\mathrm{tg}\,\,α_\mathrm{r},\]

  Similarly for x_v we get:

  \[x_\mathrm{v}=\, d\,\mathrm{tg}\,\,α_\mathrm{v}.\]

  We substitute this in the equation for Δx which gives:

  \[\mathrm{Δ}x=\, d\,\mathrm{tg}\,\,α_\mathrm{r} − d\,\mathrm{tg}\,\,α_\mathrm{v}= \, d\left(\mathrm{tg}\,\,α_\mathrm{r} − \mathrm{tg}\,\,α_\mathrm{v}\right).\]

  We calculated the angles α_č a α_f in the previous hint, so we can substitute for them and get the spectrum width.

• Notation

  b = 0,01 mm =10−5 m	groove spacing
  d = 3 m	distance between the diffraction grating and the projection screen
  k = 1	order of the maximum
  λv = 390 nm = 3,9·10−7 m	wavelength of the violet light
  λr = 790 nm = 7,9·10−7 m	wavelength of the red light
  Δx = ? (cm)	spectrum width

• Solution

  

  We denoted: d the distance between the diffraction grating and the screen, x _v the distance between the first and zero order violet maxima , α_v the angle of the first order violet maximum, x_r the distance between the first and zero order red maxima, α_r is the angle of the first order red maximum and Δx the width of the spectrum on the screen in the picture.

  To calculate the spectrum width on the screen Δx we express it using the distances x_v, x_r and angles α_v, α_r.

  \[\mathrm{Δ}x=\, x_\mathrm{r} − x_\mathrm{v}=\, d\,\mathrm{tg}\,\,α_\mathrm{r} − d\,\mathrm{tg}\,\,α_\mathrm{v}=\,d\left(\mathrm{tg}\,\,α_\mathrm{r} − \mathrm{tg}\,\,α_\mathrm{v}\right).\]

  We don’t know the angles of the maxima α_č and α_f in this equation. It holds for those angles:

  \[\sin\,α_\mathrm{r} = \, \frac{\mathrm{Δ}l_\mathrm{r}}{b} \quad \mathrm{a} \quad \sin\,α_\mathrm{v} = \, \frac{\mathrm{Δ}l_\mathrm{v}}{b}.\]

  We substitute the relation with the interference maxima for Δl and set k = 1. Substituting the wavelengths of red and violet light into the expressions we obtain:

  \[\sin\,α_r = \, \frac{λ_\mathrm{r}}{b} \quad \mathrm{a} \quad \sin\,α_v = \, \frac{λ_\mathrm{v}}{b}.\]

  We express the angles α_r a α_v:

  \[α_r = \,\arcsin\, \frac{λ_\mathrm{r}}{b} \quad \mathrm{a} \quad α_v = \,\arcsin\, \frac{λ_\mathrm{v}}{b}.\]

  We substitute it into the equation for Δx:

  \[\mathrm{Δ}x=\,\,d\left(\mathrm{tg}\,\,α_\mathrm{r} − \mathrm{tg}\,\,α_\mathrm{v}\right)=\, d\left(\mathrm{tg}\,\,\arcsin\, \frac{λ_\mathrm{r}}{b} − \mathrm{tg}\,\,\arcsin\, \frac{λ_\mathrm{v}}{b}\right)=\] \[=\, 3(\mathrm{tg}\,\,\arcsin\, \frac{7{,}9{\cdot}10^{−7}}{10^{−5}} − \mathrm{tg}\,\,\arcsin\, \frac{3{,}9{\cdot}10^{−7}}{10^{−5}})\,\dot{=}\,0{,}12\,\mathrm{m} = 12\,\mathrm{cm}.\]

• Answer

  The width of the continuous first order spectrum created on a projection screen which is 3 m behind the grating is 12 cm.

• Comment

  Thinking about magnitudes of the angles of the first order red or violet maxima we find out that those angles are very small. It holds for such angles:

  \[\sin\,\alpha\ \dot{=}\ \, \alpha\ \dot{=}\ \mathrm{tg}\,\,\alpha,\]

  where the middle equality holds for angles in radians. We will do the calculation once again with the above approximation.

  Let us express the angles and values of sin α and tg α to see that this approximation is sufficiently precise:

  \[\sin\,\alpha_\mathrm{r} =\, \frac{\lambda_\mathrm{r}}{b}= \,\frac{7{,}9{\cdot}10^{−7}}{10^\mathrm{−5}}=\,0{,}0790, \] \[\alpha_\mathrm{r}\dot=\,0{,}0791 \qquad \Rightarrow\qquad \mathrm{tg}\,\,\alpha_\mathrm{r}\ \dot{=}\ 0{,}0792,\] \[\sin\,\alpha_\mathrm{v} =\, \frac{\lambda_\mathrm{v}}{b}= \,\frac{3{,}9{\cdot}10^{−7}}{10^\mathrm{−5}}=\,0{,}0390,\] \[\alpha_\mathrm{r}\dot=\,0{,}03901 \qquad \Rightarrow\qquad\mathrm{tg}\,\,\alpha_\mathrm{v}\ \dot{=}\ \,0{,}03902,\]

   

  We get relations for angles of maxima α_r a α_v from the picture:

  \[\frac{x_\mathrm{r}}{d}=\,\mathrm{tg}\,\,\alpha_\mathrm{r}\ \dot{=}\ \,\alpha_\mathrm{r}\ \dot{=}\ \,\sin\,\alpha_\mathrm{r} = \frac{\mathrm{\Delta}l_\mathrm{r}}{b},\] \[\frac{x_\mathrm{v}}{d}=\,\mathrm{tg}\,\,\alpha_\mathrm{v}\ \dot{=}\ \,\alpha_\mathrm{v}\ \dot{=}\ \,\sin\,\alpha_\mathrm{v} = \frac{\mathrm{\Delta}l_\mathrm{v}}{b},\]

  We can substitute the equation for interference maxima Δl = kλ for Δl, set k = 1 and express x_r and x_v:

  \[\mathrm{\Delta}x=\, x_\mathrm{r} − x_\mathrm{v}=\,\frac{d}{b}\left(\lambda_\mathrm{r} − \lambda_\mathrm{v}\right)\]

  Substituting the values from the assignment:

  \[\mathrm{\Delta}x=\,\frac{3}{10^\mathrm{−5}}\cdot\left(7{,}9{\cdot}10^{−7} − 3{,}9{\cdot}10^{−7}\right)\,\mathrm{m}= \,0{,}12\,\mathrm{m}=\,12\,\mathrm{cm}.\]

  We see that the solution is the same, although we applied the approximation on the angles.