Collection of Solved Problems in Physics

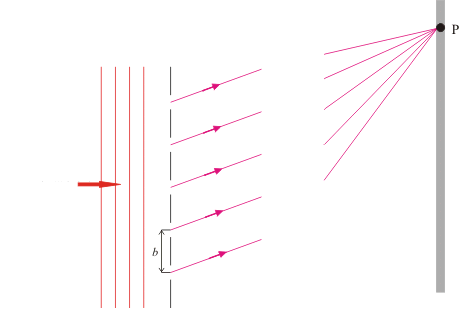
Deflection of the First Diffraction Maximum at a Grating

Task number: 1974

• Hint 1

  What is the meaning of the groove period?

• Solution of Hint 1

  The groove period is the distance between two neighbouring grooves/slits on the grating.

  

• Hint 2

  Find the path difference of rays shining from two adjacent slits onto a point on a far screen that is not located at the optical axis.

• Solution of Hint 2

  We first draw the situation when the monochromatic light passes through an idealized 5-groove grating. We draw all the light rays that fall to point P on the screen.

  

  We take the rays from two adjacent grooves and draw them in a close-up.

  We presume that our screen is far away from the grating. In that case, the rays shining onto a given point are approximately parallel.

  

  For the right-angled triangle indicated above, we can write:

  \[\mathrm{Δ}l = \,b\sin\,α,\]

  where Δl is the path difference between the rays from two adjacent slits, b is the groove period and α is the angle formed between the rays and the optical axis.

  An interference maximum or minimum may occur at point P, dependenig on the path difference of neighbouring rays.

• Hint 3

  What is the condition for two rays to produce an interference maximum?

• Solution of Hint 3

  We want to find the point P at which an interference maximum (a bright fringe) occurs. This happens when the following condition is fulfilled:

  \[\mathrm{Δ}l = k λ,\]

  where λ is the wavelength and k is the order of the maximum.

  In this task, we are looking for the first-order maximum, k = 1.

• Notation

  b = 10−2 mm = 10−5 m	Groove period
  λ = 500 nm = 5.0·10−7 m	Wavelength of the diffracted light
  k = 1	Order of the maximum
  α = ? (°)	Deflection angle from the normal

• Solution

  A monochromatic light bends (diffracts) at individual slits of the grating and an interference pattern is formed on the screen. The position of interference maxima (bright fringes) and minima (dark fringes) on the screen depends on the path differences of the rays coming out of adjacent slits of the grating.

  Let us presume that the screen is so far from the grating that the rays falling to a certain point P at the screen from different slits are approximately parallel.

  

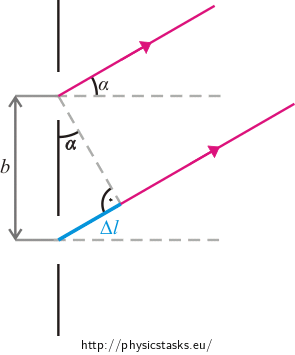
  It is then true in the indicated right-angled triangle that:

  \[\mathrm{Δ}l = \,b\sin\,α,\]

  where Δl is the path difference between rays falling to point P from two adjacent slits, b is the groove period (the distance between two adjacent slits) and α is the angle between the rays and the normal to the grating.

  We express the angle α and we get:

  \[α= \,\arcsin\, \frac{\mathrm{Δ}l}{b}.\]

  For a bright fringe (interference maximum) at point P, the path difference Δl must be:

  \[\mathrm{Δ}l = k λ,\]

  where k is the order number of the maximum; the assignment tells us to look for the first-order maxiumum, k = 1.

  We substitute the third equation into the second one, use the given values and we get:

  \[α= \,\arcsin \,\frac{λ}{b}=\,\arcsin \,\frac{5.0{\cdot}10^{−7}}{1{\cdot}10^{−5}}=\,2°52'.\]

• Answer

  The first-order maximum is deflected by 2°51′ from the perpendicual to the grating.