Collection of Solved Problems in Physics

Correct Size of the Mirror

Task number: 1962

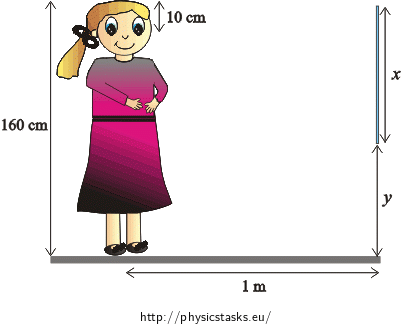
How high should a plane mirror hang vertically on a wall, so that a 160 cm tall woman standing at a distance of 1 m from the mirror, can see the whole figure of herself in the mirror? Her eyes are at a vertical distance of 10 cm from the top of her head.

At what height from the floor must be the lower edge of the mirror?

Will it be necessary to change the size of the mirror so that the woman could see her entire figure from a greater distance?

• Notation

  \(h=160\) \(\mathrm{cm}=\) \(1{.}6\) \(\mathrm{m}\)	height of the woman
  \(a=1\) \(\mathrm{m}=\) \(1{.}0\) \(\mathrm{m}\)	distance of the woman from the mirror
  \(o=10\) \(\mathrm{cm}=\) \(0{.}1\) \(\mathrm{m}\)	distance of the eyes from the top of the head
  \(x=\) \(?\)	height of the mirror
  \(y=\) \(?\)	distance of the lower edge of the mirror from the floor

• Hint 1

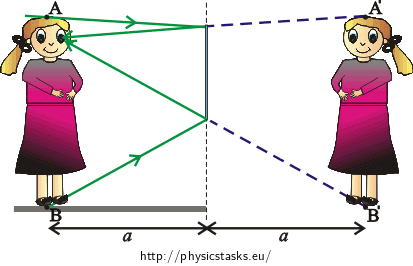
  Due to the fact that we know the properties of the image created by the plane mirror, we can draw a picture of the woman’s image. We also add the end points A and B that are projected to A' and B' to the picture.

  Draw a beam passing through point A and another one passing through point B, so that the beams are reflected into the woman’s eyes.

  

• Solution of Hint 1

  We draw a ray passing through point A, so that after the reflection from the mirror it is incident on the woman’s eyes. If we lengthen the reflected beam behind the mirror, it passes through point A'. Therefore, eyes see point A'.

  We are interested in a mirror of the smallest possible height (in which we see points A' and B'), therefore we need the beam travelling through point A to be reflected from the upper edge of the mirror.

  In case of the beam travelling through point B, we proceed similarly. We want this beam to reflect from the lower edge of the mirror.

  

  The woman sees points A' and B', which implies that she sees her entire figure.

• Hint 2

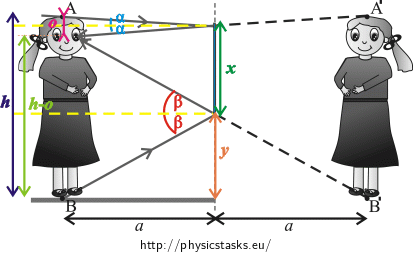
  The law of reflection tells us that the angle of incidence equals the angle of reflection (we have used it to draw the reflected rays). As it is shown in the picture, the beam from the top of the head is incident on the mirror at the angle \(α\) and is reflected to the eyes also at the angle \(α\). If the beam is incident on the mirror at the angle \(β\), it is reflected from it at the angle \(β\).

  We draw the angles \(α, β\) and all important distances (which we already know or want to determine) in the picture.

  

  Using the picture and the knowledge of geometry, determine the height of the mirror \(x\) and the distance of the lower edge of the mirror from the floor \(y\).

  How does the size of the mirror depend on the distance between the woman and the mirror?

• Solution of Hint 2

  Note:

  • the normal to the reflection surface for the beam passing through point A bisects \(o\).
  • the normal to the reflection surface for the beam passing through point B bisects \(h−o\).

  We add this information to the picture.

  

  We redraw the picture without the woman and her image for better clarity.

  

  We can see in the picture that for the height of the mirror it holds that: \[x=\frac{o}{2}+\frac{h-o}{2}=\frac{h}{2}.\]

  As it follows from this relation, the size of the mirror does not depend on the distance of the woman from the mirror.

  Using the picture, we can also determine the distance of the lower edge of the mirror from the floor: \[y=\frac{h−o}{2}.\]

  Numerical solution:

  We know from the task assignment:

  \(h=\) \(1{.}6\) \(\mathrm{m}\)

  \(o=\) \(0{.}1\) \(\mathrm{m}\)

  After the substitution, we obtain:

  \(x=\) \(\frac{1{.}6}{2} \mathrm{m}\) \(=\) \(0{.}8\) \(\mathrm{m}\) \(=\) \(80\) \(\mathrm{cm}\),

  \(y=\) \(\frac{1{.}6−0{.}1}{2} \mathrm{m}\) \(=\) \(0{.}75\) \(\mathrm{m}\) \(=\) \(75\) \(\mathrm{cm}\).

• Overall Solution

  Image of the woman and the desired mirror

  Due to the fact that we know the properties of the image created by the plane mirror, we can draw a picture of the woman’s image. We also add the end points A and B that are projected to A' and B' to the picture.

  Draw a beam passing through point A and another one passing through point B, so that the beams are reflected to the woman’s eyes. If we lengthen the reflected beam behind the mirror, it passes through point A'. Therefore, eyes see point A'.

  We are interested in a mirror of the smallest possible height (in which we see points A' and B'), therefore we need the beam travelling through point A to be reflected from the upper edge of the mirror.

  In case of the beam travelling through point B, we proceed similarly. We want this beam to reflect from the lower edge of the mirror.

  

  The woman sees points A' and B', which implies that she sees her entire figure.

   

  Height and location of the mirror quantitatively

  The law of reflection tells us that the angle of incidence equals the angle of reflection (we have used it to draw the reflected rays). As it is shown in the picture, the beam from the top of the head is incident on the mirror at the angle \(α\) and is reflected to the eyes also at the angle \(α\). If the beam is incident on the mirror at the angle \(β\), it is reflected from it at the angle \(β\).

  Note:

  • the normal to the reflection surface for the beam passing through point A bisects \(o\).
  • the normal to the reflection surface for the beam passing through point B bisects \(h−o\).

  We add this information to the picture.

  

  We redraw the picture without the woman and her image for better clarity.

  

  We can see in the picture that for the height of the mirror it holds that: \[x=\frac{o}{2}+\frac{h-o}{2}=\frac{h}{2}.\]

  As it follows from this relation, the size of the mirror does not depend on the distance of the woman from the mirror.

  Using the picture, we can also determine the distance of the lower edge of the mirror from the floor: \[y=\frac{h−o}{2}.\]

  Numerical solution:

  We know from the task assignment:

  \(h=\) \(1{.}6\) \(\mathrm{m}\)

  \(o=\) \(0{.}1\) \(\mathrm{m}\)

  After the substitution, we obtain:

  \(x=\) \(\frac{1{.}6}{2} \mathrm{m}\) \(=\) \(0{.}8\) \(\mathrm{m}\) \(=\) \(80\) \(\mathrm{cm}\),

  \(y=\) \(\frac{1{.}6−0{.}1}{2} \mathrm{m}\) \(=\) \(0{.}75\) \(\mathrm{m}\) \(=\) \(75\) \(\mathrm{cm}\).

• Answer

  The mirror has to be 80 cm high and its lower edge must be at the height of 75 cm above the floor. The size of the mirror does not need to be changed, even if the woman stands in the different distance from the mirror.

• Task to practice

  Try to think over how the situation will change, if there is a 120 cm tall boy standing in front of the mirror who has a high hat on his head (the height of the hat from the head is 40 cm). The boy’s eyes are at a vertical distance of 10 cm from the top of his head.

• Solution of Task to Practice

  From the task assignment:

  \(h=\)  \(1{.}2\) \(\mathrm{m}\) \(+\) \(0{.}4\) \(\mathrm{m}=\) \(1{.}6\) \(\mathrm{m}\),

  \(o= \)  \(0{.}4\) \(\mathrm{m}\) \(+\) \(0{.}1\) \(\mathrm{m}=\)  \(0{.}5\) \(\mathrm{m}\).

  Height of the mirror: \(x=\frac{h}{2}.\)

  Distance of the lower edge of the mirror from the floor: \(y=\frac{h−o}{2}.\)

  After the substitution we obtain:

  \(x=\) \(\frac{1{.}6}{2} \mathrm{m}\) \(=\) \(80\) \(\mathrm{cm}\),

  \(y=\) \(\frac{1{.}6−0{.}5}{2} \mathrm{m}\) \(=\) \(55\) \(\mathrm{cm}\).

  The mirror will be as high as the one in the original task, but it will be placed at a different height (the lower edge of the mirror will be at the height of \(55\) \(\mathrm{cm}\) above the floor).