Index of Refraction of a Prism

Task number: 2326

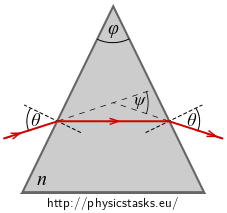
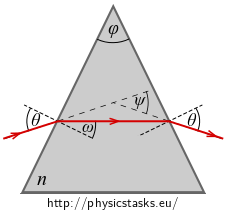
We made a measurement to determine the refractive index \(n\) of glass of a triangular prism as shown in the figure on the right.

We let a narrow beam of light hit the first boundary at an angle \(\theta\) such that it was refracted on the second boundary at the same angle \(\theta\).

We found out that the angle of deviation - which is the total deflection of a ray when passing through a prism – is \(\psi\).

Find a relation which we can use to determine the unknown index of refraction \(n\) from the measured values \(\varphi,\psi\).

Theory
When the ray is refracted on a boundary of two optical media (a and b) we can use Snell’s law of refraction:
\[ \frac{\sin \alpha}{\sin \beta} = \frac{n_b}{n_a}, \]
where \(\alpha\) is the angle of incidence, \(\beta\) the angle of refraction and \(n_a, n_b\) the indices of refraction of the optical media.
Hint 1 – law of refraction
We aim to determine the dependence of the index of refraction \(n\) on angles \(\varphi\) and \(\psi\). We can see the relation between the index of refraction and the angles from the law of refraction on the boundary – write it.
Hint 1 solution – law of refraction
Hint 1 solution – law of refraction
From the symmetry of this task, it is irrelevant which boundary we choose.

It holds for the first boundary through which the ray passes that:
\[ \frac{\sin\theta}{\sin\omega} = \frac{n}{1} \tag{1}\]
where we denoted the angle of refraction as \(\omega\) and we suppose the index of refraction of the surrounding medium to be equal to \(1\).
Hint 2 – expressing ω
We expressed the dependence of the unknown index of refraction \(n\) on angles \(\theta, \omega\) in equation (1). Although our assignment is to find the dependence on the measured values \(\varphi, \psi\).

Express angle \(\omega\) using measured angles \(\varphi, \psi\).
Hint 2 solution – expressing ω
We will express angle \(\omega\) using the measured angles.

Size of angle \(\varphi\) is the same as size of the external angle at the vertex B.

Sum of the internal angles of any rectangle, thus also rectangle ABCD, is 360°. Angles at vertices A and C are right angles. Angle at the vertex B is \(180° - \varphi\). It follows that the adjacent angle at vertex B is equal to \(\varphi\).

It holds for the isosceles \(\Delta ABC\) that:
\[ \varphi = \omega + \omega, \]
thus:
\[ \omega = \frac{\varphi}{2}. \tag{2}\]
Hint 3 – expressing θ
We expressed the dependence of the unknown index of refraction \(n\) on angles \(\theta, \omega\) in equation (1). However, our assignment is to find the dependence on the measured values \(\varphi, \psi\).

Express angle \(\theta\) using the measured angles \(\varphi, \psi\).
Hint 3 solution – e xpressingθ
We will express angle \(\theta\) using the measured angles.

It holds for angles \(\theta, \nu, \omega\) with vertex at point \(\mathrm{A}\) that:
\[ \theta = \nu + \omega. \tag{3}\]
We have expressed angle \(\omega\) using \(\varphi\) in (2). It remains to express \(\nu\) using \(\psi\).

Magnitude of the external angle \(\psi\) at the vertex \(D\) in \(\Delta ACD\) is equal to sum of the internal angles at the other vertices. Because it is an isosceles triangle it holds that:
\[ \psi = \nu + \nu. \]
Thus:
\[\nu = \frac{\psi}{2}.\tag{4}\]
Substituting (2) and (4) into (3) ve get:
\[ \theta = \nu + \omega = \frac{\psi+\varphi}{2}. \tag{5}\]
Hint 4 – final expression
Substitute the relations (2) and (5) into the law of refraction (1).
Hint 4 solution – final expression
We have found expression of angles \(\omega\) and \(\theta\):
\[ \omega = \frac{\varphi}{2}, \] \[ \theta = \frac{\psi + \varphi}{2}. \]
Substituting into the law of refraction
\[ n=\frac{\sin\theta}{\sin\omega}, \]
we get the relation which we wanted to find:
\[ n=\frac{\sin \frac{\psi + \varphi}{2} }{\sin\frac{\varphi}{2}}. \]
Complete solution
When the ray is refracted on a boundary of two optical media (a and b) we can use Snell’s law of refraction:
\[ \frac{\sin \alpha}{\sin \beta} = \frac{n_b}{n_a}, \]
where \(\alpha\) is the angle of incidence, \(\beta\) the angle of refraction and \(n_a, n_b\) the indices of refraction of the optical media.

In our case it holds that:
\[ \frac{\sin\theta}{\sin\omega} = \frac{n}{1} \]
We know from the task assignment that we want to determine the dependence of the index of refraction \(n\) on angles \(\varphi\) and \(\psi\).

We will express angle \(\omega\) using the measured angles.

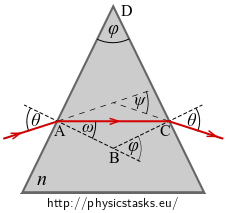
Size of angle \(\varphi\) is the same as size of the external angle at the vertex B.

Sum of the internal angles of any rectangle, thus also rectangle ABCD, is 360°. Angles at vertices A and C are right angles. Angle at the vertex B is \(180° - \varphi\). It follows that the adjacent angle at vertex B is equal to \(\varphi\).

It holds for the isosceles \(\Delta ABC\) that:
\[ \varphi = \omega + \omega, \]
thus:
\[ \omega = \frac{\varphi}{2}. \]
We will express angle \(\theta\) using the measured angles.

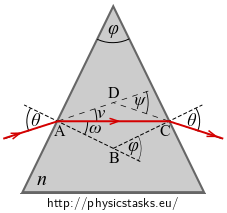
It holds for angles \(\theta, \nu, \omega\) with vertex at point \(\mathrm{A}\) that:
\[ \theta = \nu + \omega. \]
Size of the external angle \(\psi\) at vertex \(D\) in \(\Delta ACD\) is equal to sum of the internal angles at the other vertices. Because it is an isosceles triangle it holds that:
\[ \psi = \nu + \nu. \]
Thus:
\[\nu = \frac{\psi}{2}.\]
Substituting we get:
\[ \theta = \nu + \omega = \frac{\psi+\varphi}{2}. \]
Substituting the expressions of \(\varphi\) and \(\psi\) into the formula for calculating the index of refraction \(n\) we get the relation which we wanted to find:
\[ n=\frac{\sin \frac{\psi + \varphi}{2} }{\sin\frac{\varphi}{2}}. \]
Answer
The relation for calculation of the index of refraction from the measured angles is:
\[ n=\frac{\sin \frac{\psi + \varphi}{2} }{\sin\frac{\varphi}{2}}. \]
Link to an experiment
What is the angle of deviation and when is this angle minimal? Look at the experiment Refraction of Monochromatic Light With a Prism.