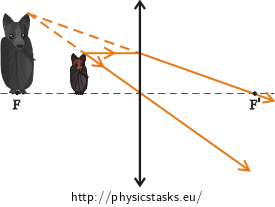
Imaging a Bat by a Spherical Mirror and a Converging Lens
Task number: 1960

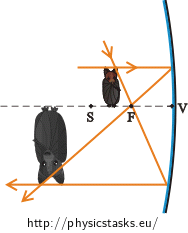
A baby bat is \(4 \mathrm{cm}\) high. Determine
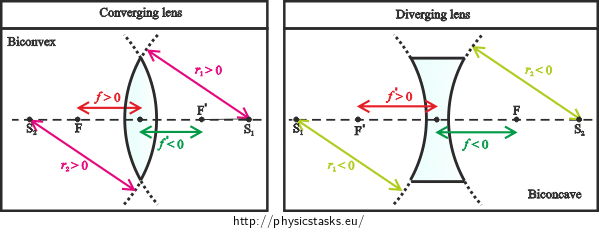
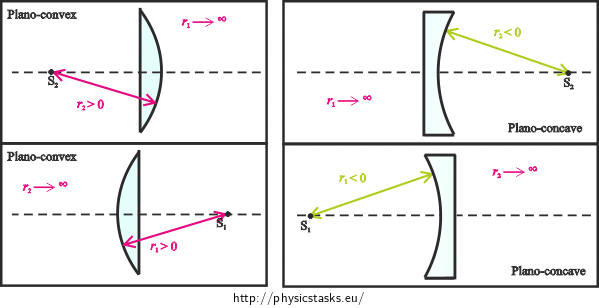
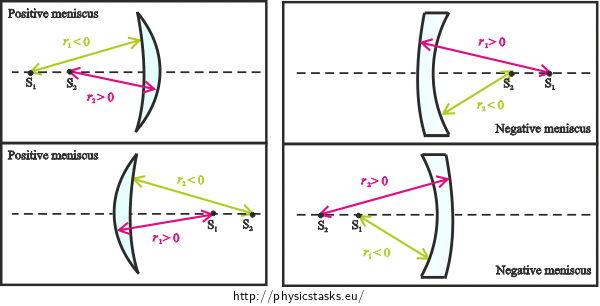
Sign convention for spherical mirrors and lenses
In further explanation we will assume that light beams always travel from the left to the right.
Note: We chose the sign convention as it is stated in grammar school textbooks. You can also encounter a different sign convention, which, however, leads to modification of geometric optics relations. Therefore, it is always necessary to adopt relations along with their sign convention.
Hint 1
Make use of the sign convention and write a notation of the problem.
Hint 2
In both cases (a) and b), we have the specified height of the object \(y \), the height of the image \(y'\) and the image distance \(a'\). We need to find a relation between these variables. Which quantity is represented by the ratio of the image’s height to the height of the object?
Hint 3
Note that the form of the imaging equation is the same for spherical mirror and lenses. Using the imaging equation and relation (3) from the previous hint, determine the focal length \(f\).
Hint 4
Now we can calculate the focal length of the converging lens. Yet, we still need to find out the relation between the focal length of the spherical mirror \(f\) and its radius of curvature \(r\). Using relation (4), express the radius of curvature \(r\).
Hint 5
Write a numerical solution of the problem. You will get the numerical solution of the question a) by substitution values in relation (5), or, in case of question b), in relation (4).
a) In compliance with the result, determine, if the mirror is convex or concave.
b) Is the value of the focal length of the converging lens positive as we expected?
Overall Solution
Notation
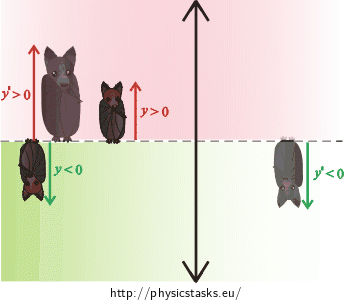
\(y= 4 \mathrm{cm}\) height of the baby bat a) Imaging by the spherical mirror \(y'=−8 \mathrm{cm}\) height of the image of the baby bat (*) \(a'= 12 \mathrm{cm}\) image distance (**) \(r= ?\) radius of curvature of the mirror (?) (*) According to the task assignment, the height of the image is twice as great as the height of the object (\(2{\cdot}4 \mathrm{cm}= 8 \mathrm{cm}\)). The value of the image’s height is negative because the image is inverted and thus is located under the optical axis.
(**) Image distance is positive because the image is in front of the mirror.
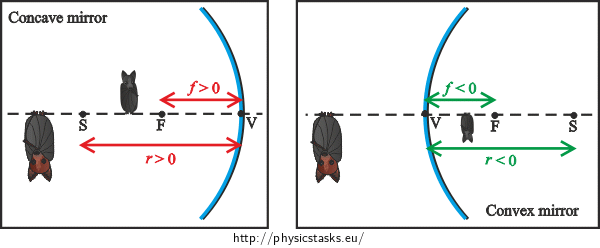
(?) According to the sign convention, the radius of curvature is positive for a concave mirror and is negative for a convex mirror.
b) Imaging by the converging lens \(y'= 8 \mathrm{cm}\) height of the image of the baby bat (***) \(a'=−12 \mathrm{cm}\) image distance (****) \(f= ?\) focal length of the converging lens (??) (***) According to the task assignment, the height of the image is twice as great as the height of the object (\(2{\cdot}4 \mathrm{cm}= 8 \mathrm{cm}\)). The value of the image’s height is positive because the image is upright and thus is located above the optical axis.
(****) Image distance is negative because the image is in front of the lens.
(??) According to the sign convention, the focal length of a converging lens is positive.
Ratio of the height of the image to the height of the object
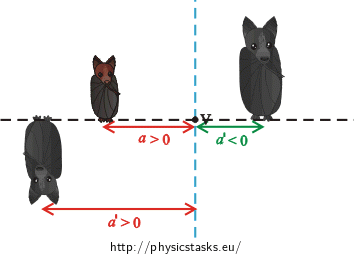
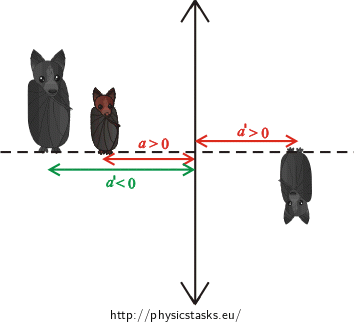
We need to find the relation between the object distance \(a\), image distance \(a'\), height of the object \(y\) and height of the image \(y'\). The ratio of the height of the image to the height of the object corresponds to the linear magnification \(Z\): \[ Z=\frac{y'}{y}.\tag{1}\]
For the linear magnification \(Z\) it is also true that: \[ Z=−\frac{a'}{a},\tag{2}\] where \(a\) is the object distance and \(a'\) is the image distance.
By comparison of (1) with (2) we get the relation between \(y \), \(y'\) and \(a'\): \[ \frac{y'}{y}=−\frac{a'}{a}.\tag{3}\] Now we have prepared a relation that we will use later in the solution.
The imaging equation
Note that the form of the imaging equation is the same both for spherical mirrors and for lenses: \[\frac{1}{a}+\frac{1}{a'}=\frac{1}{f}.\] We want to express the focal length \(f\). First, we convert fractions on the left side of the equation to the common denominator: \[\frac{a'+a}{a\cdot a'}=\frac{1}{f}.\] Thus: \[f=\frac{a\cdot a'}{a'+a}.\] Factor out \(a\) in the numerator and in the denominator: \[f=\frac{a\cdot a'}{a\left(\frac{a'}{a}+1\right)},\] \[f=\frac{a'}{\frac{a'}{a}+1}.\] Substitute for the fraction \(\frac{a'}{a}\) in accordance with relation (3): \[f=\frac{a'}{\left(−\frac{y'}{y}\right)+1}.\] Adjust the expression: \[f=\frac{a'}{\frac{−y'+y}{y}},\] \[f=\frac{a'\cdot y}{y−y'}.\tag{4}\] We have obtained an equation for calculating the focal length of the lens. In case of the spherical mirror, we do not look for the focal length, but for the radius of curvature. Therefore, in the following section, we are going to express the relation for the radius of curvature of the mirror.
Radius of curvature
The radius of curvature of the spherical mirror corresponds to twice its focal length: \[r= 2f.\] Substitute \(f\) in accordance with (4): \[r= 2\frac{a'\cdot y}{y−y'}.\tag{5}\]
Numerical solution
a) Determining the radius of curvature of the spherical mirrorAccording to the task assignment and to the sign convention:
\(y= 4 \mathrm{cm}\)
\(y'=−8 \mathrm{cm}\)
\(a'= 12 \mathrm{cm}\)
We substitute for the values in relation (5):
\(r= 2\frac{a'\cdot y}{y−y'}= 2\cdot \frac{12{\cdot} 4}{4−\left(−8\right)} \mathrm{cm}= 2\cdot \frac{48}{12} \mathrm{cm}= 8 \mathrm{cm}.\)
This is a concave mirror because the value of the radius of curvature is positive.
b) Determining the focal length of the converging lensAccording to the task assignment and to the sign convention:
\(y= 4 \mathrm{cm}\)
\(y'= 8 \mathrm{cm}\)
\(a'=−12 \mathrm{cm}\)
We substitute for the values in relation (4):
\(f=\frac{a'\cdot y}{y−y'}= \frac{−12{\cdot} 4}{4−8} \mathrm{cm}=\frac{−48}{−4} \mathrm{cm}= 12 \mathrm{cm}.\)
The value of the focal length is positive as we assumed it to be for the converging lens.
Answer
a) The radius of curvature of the spherical mirror is \( 8 \mathrm{cm}\). The mirror is concave.
b) The focal length of the converging lens is \( 12 \mathrm{cm}\).
How far in front of the lens or mirror is the bat?
We are looking for the object distance \(a\). In both cases, we use the relation: \[ \frac{y'}{y}=−\frac{a'}{a}\tag{3}\] and express the object distance from it: \[ a=−\frac{y}{y'}a'.\]
The spherical mirror
\(y= 4 \mathrm{cm}\)
\(y'=−8 \mathrm{cm}\)
\(a'= 12 \mathrm{cm}\)
Substitution:
\( a=−\frac{y}{y'}a'=−\frac{4}{\left(−8\right)}\cdot 12 \mathrm{cm}=6 \mathrm{cm}.\)
The converging lens
\(y= 4 \mathrm{cm}\)
\(y'= 8 \mathrm{cm}\)
\(a'=−12 \mathrm{cm}\)
Substitution:
\( a=−\frac{y}{y'}a'=−\frac{4}{8}\cdot \left(−12\right) \mathrm{cm}=6 \mathrm{cm}.\)
We see that the bat is in the distance of \(6 \mathrm{cm}\) in front of the spherical mirror or lens.