Collection of Solved Problems in Physics

Refraction Index of a Liquid and a Coin

Task number: 2327

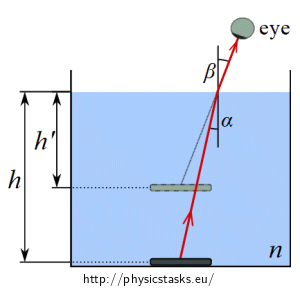
We put a coin at the bottom of a glass with a transparent liquid of height \(h\).

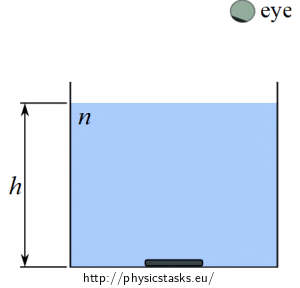
If we watch the coin not directly from above, it looks – as a result of light refraction on the liquid-air boundary - as if it was floating in the depth of \(h^\prime\) under the water surface. Draw the location of the image and determine the index of refraction \(n\) of the liquid, supposing that we observe the coin at small angles.

• Hint 1 – image of the coin

  Find the image of the coin, i.e. draw where we will see the coin.

  Light rays which are reflected at a given spot of a coin are incident on a boundary, they are refracted here and some of them continue to the eye. Draw at least two such light rays. Elongating those rays will give you location of the image of the coin which our eye sees.

• Hint 1 solution – image of the coin

  We want to know the place where our eye will see the coin. It is sufficient to deal only with its centre point. In the following image, two rays of similar direction (red colour) are drawn which are refracted on the boundary into the eye.

  

  Our eye „elongates“ the incident rays so we see the centre point of the coin in the intersection of those elongated (blue) rays.

  As a result, we see the coin not at a bottom of the glass but floating in the depth \(h^\prime\) under the water surface.

• Hint 2 – law of refraction

  Write the law of refraction for one of the rays going from the coin to our eye.

• Hint 2 solution – law of refraction

  The angles of incidence as well as the angles of refraction of the rays which we chose in the last part of the task are very similar. We will apply the law of refraction on one of the rays.

  

  We marked the angle of incidence as \(\alpha\), angle of refraction as \(\beta\).

  The index of refraction of air is approximately \(1\) so we can write the law of refraction as follows:

  \[ \frac{\sin \alpha}{\sin\beta} = \frac{1}{n}. \tag{1}\]

• Hint 3 – small angle approximation

  We assume that we watch the coin at small angles. Express the goniometric functions in the law of refraction using the known proportions \(h, h^\prime\).

• Hint 3 solution – small angle approximation

  If the angle \(\beta\) at which we watch the coin is small, i.e. \(\beta \ll 1\), the angle \(\alpha\) is also small since \(\alpha \lt \beta\). Thus:

  \[ \sin \alpha \approx \tan \alpha, \] \[ \sin \beta \approx \tan \beta, \]

  

  and thus substituting into (1) we get:

  \[\frac{\tan\alpha}{\tan\beta} \approx \frac{1}{n}.\tag{2}\]

  It follows from the marked right-angled triangles that:

  \[\tan \alpha = \frac{s}{h},\] \[\tan \beta = \frac{s}{h^\prime}.\]

  Substituting those relations into (2) gives:

  \[ \frac{\frac{s}{h}}{\frac{s}{h^\prime}} = \frac{h^\prime}{h} \approx \frac{1}{n}. \]

  From which it is easily seen (equality for small angles) that:

  \[ n = \frac{h}{h^\prime}. \]

• Complete solution

  We want to know the place where our eye will see the coin. In the following image, two rays of similar direction (red colour) are drawn which are refracted on the boundary into the eye. Our eye „elongates“ the incident rays so we see the centre point of the coin in the intersection of those elongated (blue) rays.

  

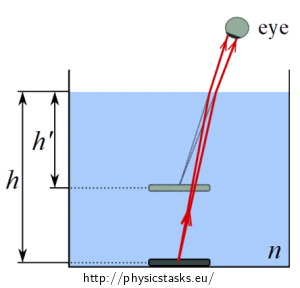
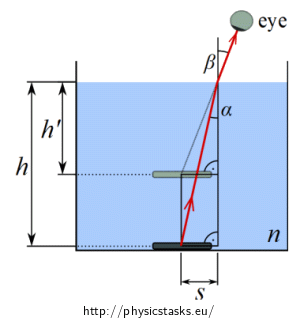
  We use the law of refraction to calculate the refraction index of the liquid. We choose one of the rays for the calculation.

  We mark the angle of incidence as \(\alpha\), angle of refraction as \(\beta\).

  

  The refraction index of air is approximately \(1\) so we can write the law of refraction as follows:

  \[ \frac{\sin \alpha}{\sin\beta} = \frac{1}{n}. \]

  If the angle \(\beta\) at which we watch the coin is small, i.e. \(\beta \ll 1\), the angle \(\alpha\) is also small since \(\alpha \lt \beta\). Thus, for small angles it holds:

  \[ \sin \alpha \approx \tan \alpha, \] \[ \sin \beta \approx \tan \beta \]

  so substituting into Snell’s law we get:

  \[\frac{\tan\alpha}{\tan\beta} \approx \frac{1}{n}.\]

  It follows from the marked right-angled triangles that:

  \[\tan \alpha = \frac{s}{h},\] \[\tan \beta = \frac{s}{h^\prime}.\]

  Substituting we get:

  \[ \frac{\frac{s}{h}}{\frac{s}{h^\prime}} = \frac{h^\prime}{h} \approx \frac{1}{n}. \]

  From which it is easily seen (equality for small angles) that:

  \[ n = \frac{h}{h^\prime}. \]

• Answer

  Supposing the refraction index of air to be \(1\), the refraction index of the liquid is:

  \[ n = \frac{h}{h^\prime}. \]

• Note

  It holds for water that \(h:h^\prime \doteq 4:3\) which implies that the index of refraction of water is approximately \(n\doteq 1{,}3\). Prove experimentally.