Collection of Solved Problems in Physics

Reflection of Light in a Glass Horseshoe

Task number: 2214

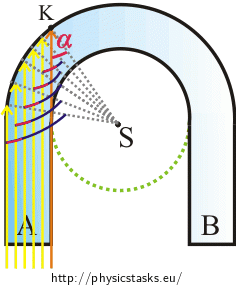
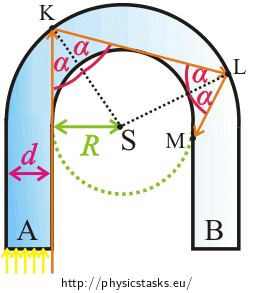
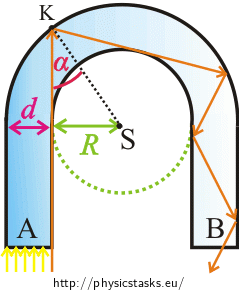
A glass rod of rectangular section is bent into a shape of a „horseshoe“ (see picture). The inner bend of the horseshoe is circular with radius \(R\) and the outer bend is also circular with radius \(R+d\).

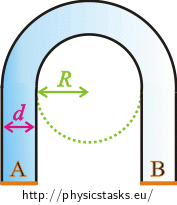
A bundle of parallel light rays is incident perpendicularly on area A. Determine the minimal value of the fraction \(\frac{R}{d}\) so that all the light from this bundle leaves the horseshoe through area B.

• Hint 1

  Because we want all the rays to go through the area B they must be totally reflected in the horseshoe. Think of when the total inner reflection occurs and write Snell’s law for the total inner reflection of light.

• Hint 1 solution

  Total inner reflection of light occurs when there is no light refracted. The light must travel from optically denser medium to optically rarer medium (thus light bends away from the normal). The maximum angle of incidence at which the light is still refracted is called the critical angle \(α_{m}\) (it holds for the angle of refraction that \(β_{m}=90°\)).

  For the total inner reflection to occur, the angle of incidence \(α\) of the ray must be greater than the critical angle \(α_{m}\): \[ α \gt α_{m}. \] If the angle of incidence is less than \(90°\) while it holds that \(α \gt α_{m}\) it also holds that: \[\sin{α} \gt \sin{α_{m}}.\tag{1}\] Snell’s law for the total inner reflection of light: \[\frac{\sin{α_{m}}}{\sin{90°}}=\frac{n_{2}}{n_{1}},\] where \(n_{2}\) is the index of refraction of the optically rarer medium and \(n_{1}\) is the index of refraction of the optically denser medium.

   

  Snell’s law for our assignment: \[\frac{\sin{α_{m}}}{\sin{90°}}=\frac{n_{a}}{n_{g}},\] where \(n_{a}\) is the index of refraction of the air and \(n_{g}\) is the index of refraction of glass in which the light rays propagate.

  It holds that \(\sin{90°}=1\) and from the tables we know that \(n_{a}  \dot= 1\). Thus: \[\sin{α_{m}}=\frac{1}{n_{g}}.\] We substitute this relation into relation (1): \[\sin{α} \gt \frac{1}{n_{g}}.\tag{2}\]

• Hint 2

  Think about if it is necessary to deal with all the light rays from the bundle.

• Hint 2 solution

  In the picture we mark the centre of two imaginary circles which form the shape of horseshoe by S. Let us now describe how the ray marked by orange colour in the picture travels. We suppose that the ray is incident on the outer circle at the angle of incidence \(α\). Let us denote the place where the ray hits the surface as K.

  The angle of incidence of other rays is always greater than \(α\). Thus, if the orange ray is totally reflected every other ray is totally reflected as well and we do not have to worry about them.

  

  That is why we can focus only on the path of the extreme ray (orange ray).

• Hint 3

  We are now going to study the path of a ray in the „bent“ part of the horseshoe.

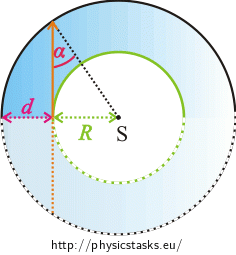
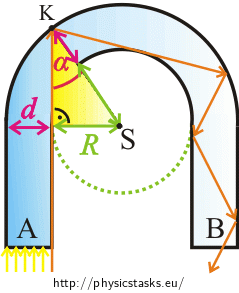
  Imagine two concentric circles with a glass annulus between them. Then imagine a ray whose trajectory is a tangent to the „inner“ circle and which is incident on the outer circle at an angle \(α\).

  

  How will the ray continue? Draw it in the picture.

• Hint 3 solution

  The ray will be reflected at an angle \(α\). We can draw a triangle in the picture (yellow triangle) – one of its interior angles is the angle of incidence. If we apply axial symmetry with the normal as the axis of symmetry on the (yellow) triangle, we get a triangle with one of interior angles equal to the angle of incidence. Since the trajectory of the incident ray is a tangent to the „inner“ circle, the trajectory of the reflected ray will also be a tangent to the „inner“ circle (from the axial symmetry of the triangles).

  

  Thus, the light ray will always be incident on the outer circle at the same angle \(α\). We would continue analogously.

  

  Let us return to the picture of the horseshoe. We found out that the trajectory of the incident ray will be tangent to the „inner“ circle. The angle of incidence and the angle of reflection will always stay the same in the whole semi-circular annulus.

  

• Note

  It may happen with different value of the fraction \(\frac{R}{d}\) that the ray is reflected only once or more than two times in the semi-circular annulus. Although it does not change the fact that the angle of incidence and the angle of reflection will always stay the same in the whole annulus.

• Hint 4

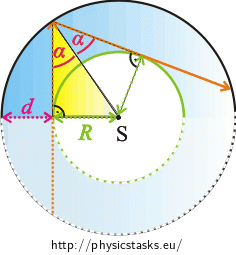
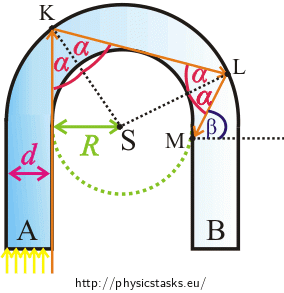
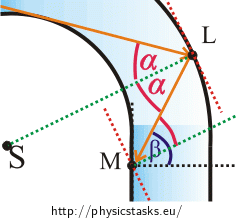
  At which angle does the ray hit point M?

  

  Will the ray be totally reflected in the point M? Draw the trajectory of the ray in the rest of the horseshoe in the picture.

• Hint 4 solution

  The ray hits the point M at an angle \( β\).

  

  It must hold that \( β \ge α \) for the total inner reflection to occur. If we move the normal (green colour in the picture) from the point L to the point M, we see that the angle \(β\) is greater than the angle \( α\).

  

  In the rest of the horseshoe, the angle of incidence and the angle of reflection will always be \(β\).

  

• Hint 5

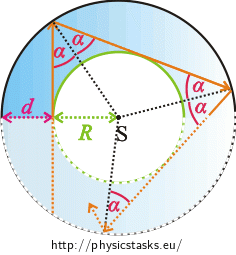
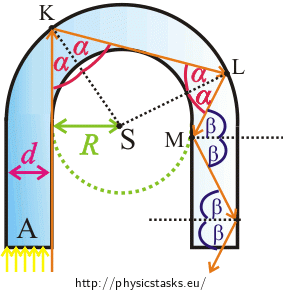
  We found out that if the ray hits the point K at an angle \(α \gt α_{m}\), it is being totally reflected until it leaves the horseshoe.

  

  Use the picture to determine the relation between the angle \(α\), radius \(R\) and the width of the horseshoe \(d\). Then use relation (2) to determine the value of the fraction \(\frac{R}{d}\).

• Hint 5 solution

  If we look closely at the right-angled triangle in the picture, we find out that the length of its hypothenuse is equal to the sum \(R+d\).

  

  Using the sine function, we get: \[\sin{α}=\frac{R}{R+d}.\tag{3}\] Remember relation (2): \[\sin{α} \gt \frac{1}{n_{g}}.\] Using relations (2) and (3), we find out that it must hold: \[\frac{R}{R+d}\gt \frac{1}{n_{g}} \] for the total inner reflection to occur. As we are also interested in the limit case (when the angle of incidence on the outer circle \(α\) is equal to the critical angle \(α_{m}\) and thus also \(\sin{α}=\sin{α_{m}}\)) we will write this inequality as: \[\frac{R}{R+d}\ge \frac{1}{n_{g}} .\] We rewrite the inequality for clarity: \[\frac{1}{n_{g}} \le \frac{R}{R+d}.\] We multiply both sides of the inequality by positive expression \(\frac{R+d}{R}\): \[\frac{1}{n_{g}}\frac{R+d}{R} \le 1.\] Simplifying the left side of the inequality we get: \[\frac{1}{n_{g}}\left(\frac{R}{R}+\frac{d}{R} \right)\le 1,\] \[\frac{1}{n_{g}}\left(1+\frac{d}{R} \right)\le 1.\] We expand the bracket: \[\frac{1}{n_{g}}+\frac{1}{n_{g}}\frac{d}{R} \le 1.\] Subtracting \(\frac{1}{n_{g}}\) from both sides of the inequality gives us: \[\frac{1}{n_{g}}\frac{d}{R} \le 1 − \frac{1}{n_{g}}.\] We find the common denominator of the right side of the inequality: \[\frac{1}{n_{g}}\frac{d}{R} \le \frac{n_{g}−1}{n_{g}}.\] We multiply both side of the inequality by \(n_{g}\): \[\frac{d}{R} \le n_{g}−1.\] We flip the fractions: \[\frac{R}{d} \ge \frac{1}{ n_{g}−1}. \]

  Numerical solution

  We find the value of the refraction index of glass in tables \(n_{g} = 1{,}5\) and substitute it into equation: \[\frac{R}{d} \ge \frac{1}{ 1{,}5−1}, \] \[\frac{R}{d} \ge 2. \]

• Complete solution

  Total internal reflection

  Because we want all the rays to go through area B they must be totally reflected in the horseshoe.

  For total inner reflection to occur, the angle of incidence \(α\) of the ray must be greater than the critical angle \(α_{m}\): \[ α \gt α_{m}. \] If the angle of incidence is less than \(90°\) while it holds that \(α \gt α_{m}\) it also holds that: \[\sin{α} \gt \sin{α_{m}}.\tag{1}\]

   

  Critical angle is such an angle when the ray is still refracted. The angle of refraction is \(90°\). In this case we write Snell’s law as: \[\frac{\sin{α_{m}}}{\sin{90°}}=\frac{n_{a}}{n_{g}},\]

  where \(n_{a}\) is the index of refraction of the air and \(n_{g}\) is the index of refraction of glass in which the light rays propagate.

  It holds that \(\sin{90°}=1\) and from the tables we know that \(n_{a}  \dot= 1\). Thus: \[\sin{α_{m}}=\frac{1}{n_{g}}.\] We substitute this relation into relation (1): \[\sin{α} \gt \frac{1}{n_{g}}.\tag{2}\]

   

  One ray is enough

  We do not have to care about all the rays from the light bundle. It is sufficient to work with the extreme (orange) ray. If the orange ray is totally reflected every other ray is totally reflected as well (other rays hit the outer circle at a greater angle than is the angle of incidence of the orange ray).

  

  Thus, if the orange ray is totally reflected when it hits the glass-air boundary for the first time, it is totally reflected in the whole horseshoe. (See Hint 3 a Hint 4.)

   

  Minimal value of the fraction \(\frac{R}{d}\)

  If we look closely at the right-angled triangle in the picture, we find out that the length of its hypothenuse is equal to the sum \(R+d\).

  

  Using the sine function, we get: \[\sin{α}=\frac{R}{R+d}.\tag{3}\] Remember relation (2): \[\sin{α} \gt \frac{1}{n_{g}}.\] \[\frac{R}{R+d}\gt \frac{1}{n_{g}} .\] As we are also interested in the limit case (when the angle of incidence on the outer circle \(α\) is equal to the critical angle \(α_{m}\) and thus also \(\sin{α}=\sin{α_{m}}\)), we will write this inequality as: \[\frac{R}{R+d}\ge \frac{1}{n_{g}} .\] We rewrite the inequality for clarity: \[\frac{1}{n_{g}} \le \frac{R}{R+d}.\] We multiply both sides of the inequality by positive expression \(\frac{R+d}{R}\): \[\frac{1}{n_{g}}\frac{R+d}{R} \le 1.\] We simplify the inequality to get \(\frac{R}{d}\) on the left side: \[\frac{1}{n_{g}}\left(\frac{R}{R}+\frac{d}{R} \right)\le 1,\] \[\frac{1}{n_{g}}\left(1+\frac{d}{R} \right)\le 1,\] \[\frac{1}{n_{g}}+\frac{1}{n_{g}}\frac{d}{R} \le 1,\] \[\frac{1}{n_{g}}\frac{d}{R} \le 1 − \frac{1}{n_{g}},\] \[\frac{1}{n_{g}}\frac{d}{R} \le \frac{n_{g}−1}{n_{g}},\] \[\frac{d}{R} \le n_{g}−1,\] \[\frac{R}{d} \ge \frac{1}{ n_{g}−1}. \]

  Numerical solution

  We find the value of refraction index of glass in tables \(n_{g} = 1{,}5\) and substitute it into equation: \[\frac{R}{d} \ge \frac{1}{ 1{,}5−1}, \] \[\frac{R}{d} \ge 2. \]

• Answer

  The minimal value of the fraction \(\frac{R}{d}\) must be equal to two for the total internal reflection to occur in the horseshoe.

• Link to an experiment

  An experiment showing the total internal reflection is described in Total Internal Reflection in a Stream of Water.