Interference of Two Plane Waves Propagating in Different Directions
Task number: 1966
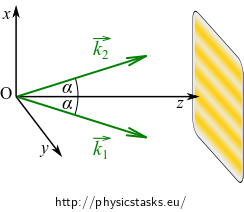
Two plane waves of the same freqency and amplitude propagate through vacuum with an angle of \(2\alpha\) formed between their wave vectors \(\vec{k}_1,\vec{k}_2\). Calculate and describe the layout of the density of electric energy of the resulting electromagnetic wave on a screen that is perpendicular to the sum wave vector \((\vec{k}_1 + \vec{k}_2)\).
Presume that the amplitude of the electric field of both waves is perpendicular to the plane given by the wave vectors \(\vec{k}_1\) and \(\vec{k}_2\). Use the following complex description of the waves:
\[ \begin{eqnarray} \vec{E}_1 &=& \vec{E}_0 e^{i(\omega t - \vec{k}_1 \cdot \vec r)},\\ \quad \vec{E}_2 &=& \vec{E}_0 e^{i(\omega t - \vec{k}_2 \cdot \vec r)}. \end{eqnarray} \]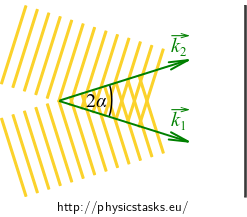
Theory
One must understand the complex description of the plane wave description to solve the task:
\[ \vec{E} = \vec{E}_0 e^{i(\omega t - \vec{k} \cdot \vec r)}, \]where \(\vec{k}\) is the wave vector aiming in the direction of propagation of the wave and has the amplitude of the angular wave number \(k = \frac{2\pi}{\lambda}\). A detailed description of the complex description of the plane wave can be found in the last section of this task.
We use Euler’s formula for the complex exponential function
\[e^{i\varphi} = \cos \varphi + i \sin \varphi.\]The density of the electric energy of an electromagnetic wave in vacuum can be calculated using the complex notation as follows:
\[w_\mathrm{E} = \frac{1}{4}\varepsilon_0\, \vec{E}\cdot\vec{E}^*.\]Hint 1 — electric field on the screen
Our aim is to assess the density of the electric energy of the resulting electromagnetic wave in vacuum:
\[w_\mathrm{E} = \frac{1}{4}\varepsilon_0\, \vec{E}\cdot\vec{E}^*.\]This implies that we need to caclulate the electric field \(\vec{E}\) of the resulting wave. Find it as the superposition (sum) of the two interfering waves.
Hint 2 — Interference pattern
The intensity of light on the screen is proportional to the electric energy density of the wave at the given point. Describe the resulting interference pattern through by analysis of the calculated function \(w_\mathrm{E}(x)\).
Solution
We have given the two waves with their electric fields:
\[\vec{E}_1 = \vec{E}_0 e^{i(\omega t - \vec{k}_1 \cdot \vec r)}, \quad \vec{E}_2 = \vec{E}_0 e^{i(\omega t - \vec{k}_2 \cdot \vec r)}.\]We get the electric field of the resulting wave as a superposition of the source waves:
\[\vec{E} = \vec{E}_1 + \vec{E}_2 = \vec{E}_0 e^{i\omega t}\big( e^{-i\vec{k}_1 \cdot \vec{r}} + e^{-i\vec{k}_2 \cdot \vec{r}} \big).\]This electric field is to be substituted into the definition of the density of electric energy:
\[w_\mathrm{E} = \frac{1}{4}\varepsilon_0\, \vec{E}\cdot\vec{E}^\star.\]Let us first calculate the scalar product of the resulting field and of its complex conjugate
\[\vec{E} = \vec{E}_0 e^{i\omega t}\big( e^{-i\vec{k}_1 \cdot \vec{r}} + e^{-i\vec{k}_2 \cdot \vec{r}} \big) \quad \mathrm{and} \quad \vec{E}^\star = \vec{E}_0 e^{-i\omega t}\big( e^{i\vec{k}_1 \cdot \vec{r}} + e^{i\vec{k}_2 \cdot \vec{r}} \big). \]which yields
\[ \vec{E}\cdot \vec{E}^\star = E_0^2 e^{i\omega t - i\omega t} \big( e^{-i\vec{k}_1 \cdot \vec{r}} + e^{-i\vec{k}_2 \cdot \vec{r}} \big)\big( e^{i\vec{k}_1 \cdot \vec{r}} + e^{i\vec{k}_2 \cdot \vec{r}} \big)= \] \[ =E_0^2 \left( e^{-i(\vec{k}_1 -\vec{k}_1) \cdot \vec{r}} + e^{ i(\vec{k}_2 -\vec{k}_1) \cdot \vec{r}} + e^{-i(\vec{k}_2 -\vec{k}_1) \cdot \vec{r}} + e^{-i(\vec{k}_2 -\vec{k}_2) \cdot \vec{r}} \right)= \] \[ = E_0^2 \left( 1 + e^{ i(\vec{k}_2 -\vec{k}_1) \cdot \vec{r}} + e^{-i(\vec{k}_2 -\vec{k}_1) \cdot \vec{r}} + 1 \right) \]We rewrite the complex exponential using Euler’s formula \(e^{i\varphi} = \cos \varphi + i \sin \varphi \)
\[ \small{= E_0^2 \left[ 2 + \cos \vec{r}\cdot(\vec{k}_2 -\vec{k}_1) + i\sin\vec{r}\cdot (\vec{k}_2 -\vec{k}_1) + \cos \vec{r}\cdot (\vec{k}_2 -\vec{k}_1) - i\sin \vec{r}\cdot (\vec{k}_2 -\vec{k}_1) \right] = } \] \[ =E_0^2 \left[ 2 + 2\cos \left(\vec{r}\cdot \left(\vec{k}_2 -\vec{k}_1\right)\right) \right] = 2E_0^2 \left[ 1 + \cos \left(\vec{r}\cdot \left(\vec{k}_2 -\vec{k}_1\right)\right) \right]. \]And we get upon substituting into the formula of the electric energy density:
\[ w_\mathrm{E} = \frac{1}{4}\varepsilon_0\, \vec{E}\cdot\vec{E}^\star = \frac{E_0^2}{2}\varepsilon_0 \left[1 + \cos \left(\vec{r}\cdot (\vec{k}_2 -\vec{k}_1)\right) \right]. \]Let us separately treat the scalar product \(\vec{r}\cdot (\vec{k}_2 -\vec{k}_1)\) in the argument of the cosine.
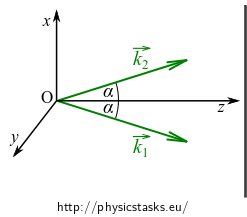
The scalar product is simple when we orient the cartesian coordinate system as indicated in the figure above:
\[ \vec{r}\cdot (\vec{k}_2 -\vec{k}_1) = x(k_{2x} - k_{1x})+ y(\underbrace{k_{2y}}_{0} - \underbrace{k_{1y}}_{0})+ z(\underbrace{k_{2z} - k_{1z}}_{0}) = x(k_{2x} - k_{1x}), \]because in this coordinate system, the y components of the wave vectors of the two waves are zero and their z components are identical.
The two waves have the same frequency and the magnitudes \(k\) of their wave vectors thus are also the same.
The following figure shows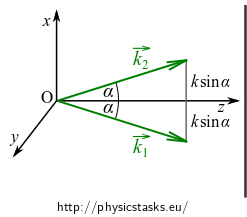
that the difference of the x components of the two wave vectors is \(2k\sin\alpha\), which gives us the scalar product:
\[ \vec{r}\cdot (\vec{k}_2 -\vec{k}_1) = x(k_{2x} - k_{1x}) = 2kx\sin\alpha. \]Using the above derived scalar product, we get the final formula for the density of the electric energy of the resulting wave:
\[ w_\mathrm{E}= \frac{E_0^2}{2}\varepsilon_0 \left[ 1 + \cos (2kx\sin\alpha) \right]. \]The electric energy density does change only along the coordinate lying in the plane defined by the wave vectors of the two initial waves, which is the x (vertical) coordinate in our coordinate system. The energy density on the screen does not change along the horizontal coordinate (the y axis, aiming perpendicular to the picture plane).
Using the goniometric identity \(\frac{1+\cos \varphi}{2} = \cos^2 \frac{\varphi}{2}\) in addition, we get the following formula for the density of electric energy on the screen:
\[w_\mathrm{E}(x) = E_0^2\,\varepsilon_0 \,\frac{1 + \cos (2kx\sin\alpha)}{2} = E_0^2\,\varepsilon_0\, \cos^2 (kx\sin\alpha).\]The interference pattern, in the sense of the relative illuminance of the screen, is thus given by the function:
\[I_r(x) = \cos^2 (kx\sin\alpha).\]The graph of the function is:
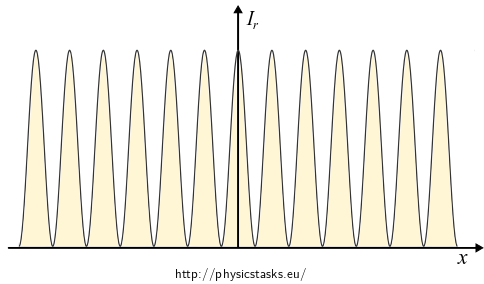
Which means that fringes directed along the \(y\) axus appear on the screen.
Calculate what the width of the interference fringes depends on. We understand the width of the fringes as the distance between the nearst minima. The intensity of light on the screen is minimal for
\[\cos^2 (kx\sin\alpha) = 0, \quad\text{ tj. když }\quad kx\sin\alpha = \frac{\pi}{2} + m\pi,\quad m\in\mathbb{Z}. \]To find the distance between two subsequent minima, we write this condition for the positions \(x_1\) and \(x_2\) of the \(m\)th and \((m+1)\)th minimum
\[\begin{eqnarray} kx_1\sin\alpha &=& \frac{\pi}{2} + m\pi \\ kx_2\sin\alpha &=& \frac{\pi}{2} + (m+1)\pi, \end{eqnarray}\]we subtract the equations
\[k(\underbrace{x_2 - x_1}_{\Delta x}) \sin\alpha = \pi\]wnd we express the fringe width:
\[\Delta x = \frac{\pi}{k\sin\alpha}.\]We get the final formula after substituting \(\frac{2\pi}{\lambda}\) for the mangitude of the wave vector \(k\)
\[\Delta x = \frac{\lambda}{2\sin\alpha}. \]It follows from this relation, that the interference pattern gets more sparse with longer wavelengths and gets denser with increasing angle between the two waves.
Answer
The density of the electric energy on the screen is:
\[w_\mathrm{E}(x) = E_0^2\,\varepsilon_0 \cos^2 (kx\sin\alpha), \]The relative illuminance of the screen is given by the function
\[I_r(x) = \cos^2 (kx\sin\alpha).\]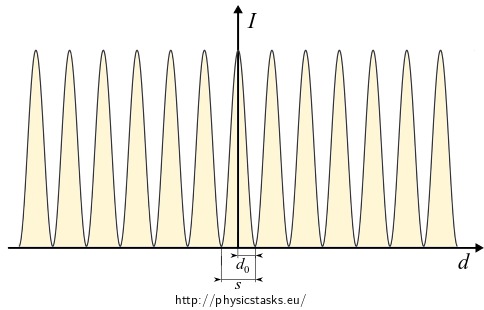
The width of the interference fringes (separation of the minima of the relative illuminance) is
\[\Delta x = \frac{\lambda}{2\sin\alpha}. \]The interference pattern gets more sparse with longer wavelengths and gets denser with increasing angle between the two waves.
Note: “Building“ the plane wave (complex formalism)
We derive the complex equation of a plane wave by gradual generalization of the equation of a one-dimensional wave in this section.
One may remember from the high school that the wave equation of a one-dimensional wave can be described with the equation
\[y(x,t) = y_0 \cos \left[\omega \left( t - \frac{x}{v}\right)\right].\]The equation above is nothing more than a generalization of the equation of a harmonic oscillator to a harmonic wave. It takes time \(\frac{x}{v}\) for the wave to travel the distance \(x\) from the source at the propagation speed \(v\). The displacement of the point at the distance \(x\) from the source at a given time \(t\) is thus the same as the displacement of the source before the time \(\frac{x}{v}\) that the wave needs to propagate from the source to that point. The displacement of any point at any time is described by the general argument of the cosine function \(t - \frac{x}{v}\).
In our optical case, there oscillates the magnitude of vector of electric field \(\vec{E}\) instead of the geometrical displacement of a physical point. The speed of light is usually denoted \(c\), and thus we get
\[\vec{E} = \vec{E}_0 \cos \left[\omega \left( t - \frac{x}{c}\right)\right].\]We have here one vector of the electric field for every point along the line of propagation. To build a plane wave, we need to attirbute the same vector to all points in the plane perpendicular to the direction of propagation.
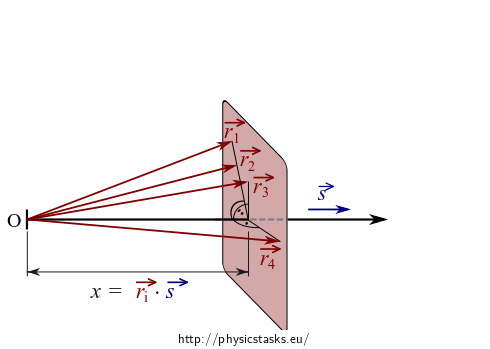
The perpendicular plane consists of points whose position vectors \(\vec{r}\) have the same projection \(x\) to the direction of propagation \(\vec{s}\). The projection magnitude is defined by the scalar product:
\[\vec{r} \cdot \vec{s} = x.\]We thus obtain the wave equation of a plane wave in the form:
\[\vec{E} = \vec{E}_0 \cos \left[\omega \left( t - \frac{\vec{r} \cdot \vec{s}}{c}\right)\right] = \vec{E}_0 \cos \left(\omega t - \omega \frac{\vec{r} \cdot \vec{s}}{c}\right).\]The second term of the argument is complicated enough. Let us simplify it:
\[\omega \frac{\vec{r} \cdot \vec{s}}{c} = 2\pi \nu \frac{\vec{r} \cdot \vec{s}}{c} = 2\pi \frac{c}{\lambda} \frac{\vec{r} \cdot \vec{s}}{c} = \underbrace{\frac{2\pi}{\lambda}\vec{s}}_{\mathrm{ozn.}\,\vec{k}} \cdot\vec{r} = \vec{k}\cdot\vec{r}.\]We have used the relations \(\omega = 2\pi \nu\) and \(\lambda = \frac{c}{\nu}\). In this way we have introduced the wave vector \(\vec{k}\), that aims in the direction of propagation and has the magnitude \(\frac{2\pi}{\lambda}\) for the plane harmonic wave.
The plane wave has now a relatively elegant form:
\[\vec{E} = \vec{E}_0 \cos \left(\omega t - \vec{k} \cdot \vec{r} \right),\]however, it is clumsy for calculations — such as superposition of waves — it leads to sums of goniometric functions with different arguments. For this reason we introduce the complex representation of the wave. Let us work in full generality, without omitting the initial phase \(\varphi_0\) in the argument:
\[\vec{E} = \vec{E}_0 \cos \left(\omega t - \vec{k} \cdot \vec{r} + \varphi_0 \right).\]We add the following imaginary vector function to the formula above:
\[i \vec{E}_0 \sin \left(\omega t - \vec{k} \cdot \vec{r} + \varphi_0 \right),\]and we obtain the complex wave
\[\overset{\sim}{\vec E} = \vec{E}_0 \cos \left(\omega t - \vec{k} \cdot \vec{r} + \varphi_0 \right) + i \vec{E}_0 \sin \left(\omega t - \vec{k} \cdot \vec{r} + \varphi_0 \right). \]Using the definition of the complex exponential \(e^{i\alpha} = \cos\alpha + i\sin \alpha\), we get
\[ \overset{\sim}{\vec E} = \vec{E}_0 e^{i\left(\omega t - \vec{k} \cdot \vec{r} + \varphi_0 \right)} = \underbrace{\vec{E}_0 e^{i\varphi_0 }}_{\mathrm{ozn.\,}\overset{\sim}{\vec{E}_0}} e^{i\left(\omega t - \vec{k} \cdot \vec{r}\right)} = \overset{\sim}{\vec{E}_0} e^{i\left(\omega t - \vec{k} \cdot \vec{r}\right)}. \]where we have introduced the complex amplitude vector \(\overset{\sim}{\vec{E}_0}\), that includes not only the information about the amplitude of the wave but also its initial phase.
Summing of complex waves in linear optics is easily accomplished with exponential functions. After performing the needed mathematical combinations of the source waves in the complex formalism, we look at the real part of the resulting complex wave, as given below, to assess the real (measurable) properties of the wave
\[\vec{E} = \mathrm{Re\,} \overset{\sim}{\vec{E}}.\]The symbol \(\sim\) is usually not written above complex quantities (it is mostly used in textbooks during implementing of the complex formalism only). One recognizes that a quantity is complex when it is expressed using the complex exponential. We also omit the complex tilde symbol in this task, except for this single explanatory section.
Let us note that the complex formalism is only a mathematical improvement in this case, the imaginary part has no physically measurable meaning.



