Magnification of Microscope
Task number: 1963
Linear magnification of the objective lens of a microscope is \(30\), angular magnification of the ocular lens is \(5\) and the optical tube length of the microscope is \(15 \mathrm{cm}\). Determine the magnification of the microscope, if the object is observed with the eye without accommodation. Then determine the focal length of the objective lens and of the eyepiece (ocular lens).
Notation
\(Z_{1}= 30\) linear magnification of the objective lens \(γ_{2}=5\) angular magnification of the ocular lens \(Δ=15 \mathrm{cm}= 0{.}15 \mathrm{m}\) optical tube length of the microscope \(γ= ?\) magnification of the microscope \(f_{1}= ?\) focal length of the objective lens \(f_{2}= ?\) focal length of ocular lens Hint 1
What is the microscope composed of and how does it work?
Hint 2
What is the relation between the total magnification of the microscope \(γ\), linear magnification of the objective lens \(Z_{1}\) and the angular magnification of the ocular lens \(γ_{2}\)?
Hint 3
What is an optical tube length \( Δ\)?
Hint 4
Deduce the relation for the linear magnification of the objective lens. Then determine the focal length of the lens.
Hint 5
What is the angular magnification of the ocular lens? How do we calculate it? Determine the focal length of the ocular lens.
Overall Solution
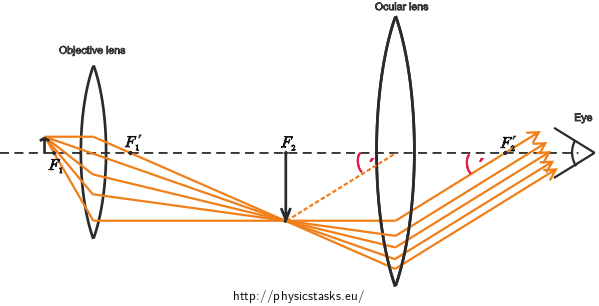
Picture of the microscope
The microscope consists of two converging lenses (objective and ocular lens).
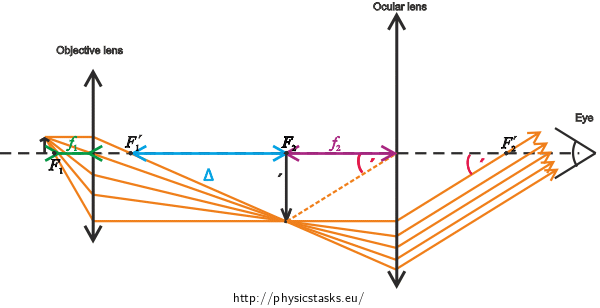
Description of the picture
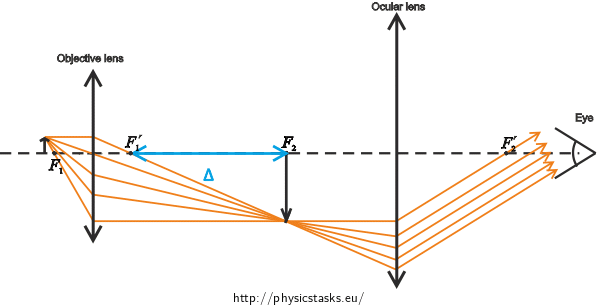
\(F_{1}\) object focal point of the objective lens\(y\)height of the object\(F'_{1}\) image focal point of the objective lens\(y'\)height of the image created by the objective lens\(F_{2}\) object focal point of the ocular lens\(f_{1}\)focal length of the objective lens\(F'_{2}\) image focal point of the ocular lens\(f_{2}\)focal length of the ocular lens\(τ'\) zvětšený zorný úhel\(Δ\)optical tube lengthTotal magnification of the microscope
We obtain the total magnification of the microscope as the product of the linear magnification of the objective lens and the angular magnification of the eyepiece. Thus: \[γ=Z_{1}\cdot γ_{2}\tag{1}\]
Linear magnification of the objective lens and its focal length
Linear magnification of the objective lens \( Z_{1}\) tells us how many times the image created by the objective lens is larger than the projected object, thus it applies: \[Z_{1}=\frac{y'}{y},\tag{2}\] where \(y'\) is the height of the image and \(y\) is the height of the object.
We determine the ratio of the height of the image to the height of the object.
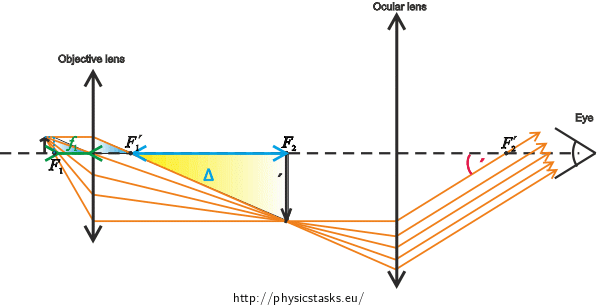
The yellow triangle is similar to the blue triangle. From the similarity it follows that: \[\frac{y'}{Δ}=\frac{y}{f_{1}},\] where \(f_{1}\) is the focal length of the objective lens. We express the ratio of the height of the object to the height of the image: \[\frac{y'}{y}= \frac{Δ}{f_{1}}.\] And in accordance with (2): \[Z_{1}= \frac{Δ}{f_{1}}.\] Therefrom we express the focal length of the objective lens: \[f_{1}= \frac{Δ}{Z_{1}}.\tag{3}\]
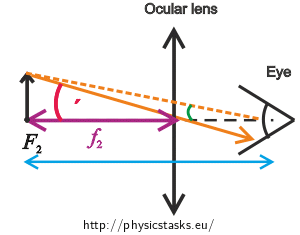
Angular magnification of the ocular length and its focal length
The ocular lens of the microscope works as a magnifying glass. It applies: \[γ_{2}=\frac{τ'}{τ}.\tag{4}\]
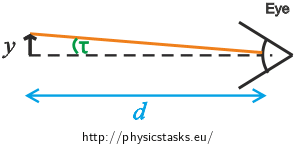
We draw a picture from which we can determine the value of the angle of view \(τ\) at which we observe the object of the height \(y\) from the conventional distance of distinct vision \(d\) with the naked eye.
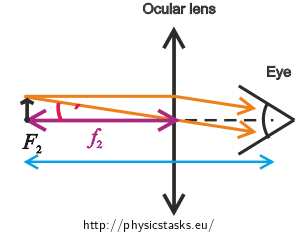
Now we place the ocular lens between the object and the eye so that the object is at the object focal point of the ocular lens. Angle at which we observe the object will increase (magnified angle of view \(τ'\)).
We deduce from the picture that if we observe the object with the naked eye it holds true: \[\mathrm{tg}\,{τ}=\frac{y}{d}.\] Since angle \(τ\) is very small, we can assume that \(\mathrm{tg}\,{τ} \dot= τ\) and thus we can write: \[τ=\frac{y}{d}.\tag{5}\]
If we observe the object trough the eyepiece, we can deduce the relation for the magnified angle of view \(τ'\): \[\mathrm{tg}\,{τ'}=\frac{y}{f_{2}}.\] The magnified angle of view \(τ'\) is small and thus we can write: \[τ'=\frac{y}{f_{2}}.\tag{6}\]
We substitute for relations (5) and (6) in the relation for the angular magnification of the ocular lens (4) and adjust the relation:
\[γ_{2}=\frac{τ'}{τ}=\frac{\frac{y}{f_{2}}}{\frac{y}{d}},\] \[γ_{2}=\frac{d}{f_{2}}.\]
We express the focal length of the ocular lens: \[f_{2}=\frac{d}{γ_{2}}.\tag{7}\]
Numerical solution
Known from the task assignment:
\(Z_{1}=30\)
\(γ_{2}=5\)
\(Δ=0{.}15 \mathrm{m}\)
We look up the conventional distance of distinct vision in the Tables:
\(d= 0{.}25 \mathrm{m}\)
We substitute for the values in the following relationships:
for the total magnification of the microscope (1):
\(γ=Z_{1} \cdot γ_{2} = 30 {\cdot} 5=150.\)
for the focal length of the objective lens (3):
\(f_{1}= \frac{Δ}{Z_{1}}=\frac{0{.}15}{30} \mathrm{m}=5{\cdot}10^{−3} \mathrm{m}=5 \mathrm{mm}.\)
for the focal length of the ocular lens (7):
\(f_{2}=\frac{d}{γ_{2}}=\frac{0{.}25}{5} \mathrm{m}=5{\cdot}10^{−2} \mathrm{m}=50 \mathrm{mm}.\)
Answer
The magnification of the microscope is \(150\). The focal length of the objective lens is \(5 \mathrm{mm}\) and the focal length of the ocular lens is \(50 \mathrm{mm}\).