Electric Intensity at a Vertex of a Triangle
Task number: 1549
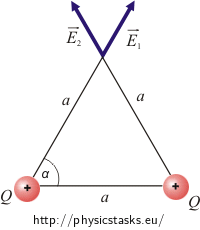
Two positive point charges of a charge 1 µC are placed at two vertices of an equilateral triangle of a side 0.5 m.
Determine the electric field intensity at the third vertex of this triangle.
Hint 1
The overall electric field intensity is obtained by summing the intensities of the two charges. Draw a picture.
Hint 2
The vector of electric intensity has the same direction as the force that would act on a positive charge at a given point.
Figure
Analysis
The total electric intensity at a vertex of a triangle is given by the vector sum of the intensities of the individual charges.
The charges are of the same size and are at the same distance from the point in which we want to determine the electric intensity. This means that both vectors of electric intensity are of the same size. The direction of the vector of electric intensity is the same as the direction of the electric force that would act on a positive charge (a "test" charge) at the vertex of the triangle. In the case of the positive charges, the vector points "from" the charges.
Solution
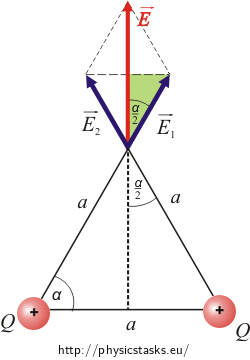
The overall intensity is obtained by the vector sum of both intensities created by each individual point charge.
The intensities \(\vec{E}_1\) and \(\vec{E}_2\) have the same size, because both charges are of the same size and have equal distance from the point where the intensity is measured. Since the charges are positive, the intensity vectors point from them.
We know, that the triangle is equilateral, therefore we can determine the angle α = 60°
We express the cosine of angle \(\frac{\alpha}{2}\) from the "green" right-angled triangle.
\[\cos{\frac { \alpha}{2}}\,=\,\frac{\frac {E}{2}}{E_1}\]and evaluate the unknown overall intensity E
\[E\,=\,2E_1\cos \frac{\alpha}{2}\,.\tag{*}\]We determine the intensity E1 from the relation:
\[E_1\,=\,k \, \frac{Q}{r^2}\, ,\]where r is the distance of the charges. In our case, we have denoted a as the distance of the charges. We substitute this relation into (*).
\[E\,=\,2k\, \frac {Q}{a^2} \,\cos \frac{\alpha}{2}\]Given values and numerical substitution
\[ \begin{eqnarray} a\,&=&\,0.5 \,\mathrm{m}\\ Q\,&=&\,1\,\mathrm{\mu C}\,=\,10^{-6}\,\mathrm{C}\\ E\,&=&\,?\,\left(\mathrm{kV\,m^{-1}}\right) \end{eqnarray}\]From The Handbook of Chemistry and Physics:
\[k\,=\, 9 {\cdot} 10^9\,\mathrm{kg\,m^2\,s^{-2}\,C^{-1}}\]
\[ \begin{eqnarray} E\,&=&\,2k\, \frac {Q}{a^2} \,\cos \frac{\alpha}{2}\\ E\,&=&\,2 \,\cdot \,9 {\cdot} 10^9 \,\cdot\, \frac {10^{-6}}{0.5^2}\,\cdot\, \cos \frac{60^\circ}{2}\, \mathrm{V\,m^{-1}}\,=\,\frac{18 {\cdot} 10^3}{0.25} \cdot \frac {\sqrt 3}{2}\, \mathrm{V\,m^{-1}}\\ E\,&=&\,6.2 {\cdot}10^4 \, \mathrm{V\,m^{-1}}\,=\,62 \, \mathrm{kV\,m^{-1}} \end{eqnarray}\]Answer
The vector of electric intensity at the third vertex of the triangle points upwards and its size is
\[E\,=\,2k\, \frac {Q}{r^2} \,\cos \frac{\alpha}{2}\,=\,62 \, \mathrm{kVm^{-1}}\,.\]What changes if both charges are negative?
The vectors \(\vec{E}_1\) and \(\vec{E}_2\) are still of the same size, as the charges are of the same size and at equal distance. But the vectors point in the opposite direction, because the charges are negative.
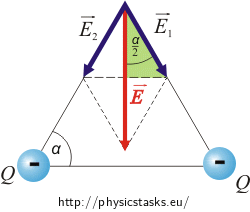
The method of calculation would be the same.
The total intensity would thus have the same size but opposite direction.