Transformer
Task number: 1548
A transformer has 500 turns of the primary winding and 10 turns of the secondary winding.
a) Determine the secondary voltage if the secondary circuit is open and the primary voltage is 120 V.
b) Determine the current in the primary and secondary winding, given that the secondary winding is connected to a resistance load 15 Ω?
Given values
In the assignment it is given:
Number of turns of the primary coil: N1 = 500 Number of turns of the secondary coil: N2 = 10 a) Primary voltage: U1 = 120 V b) Secondary winding connected to a resistance load: R = 15 Ω Unknown quantities we need to determine:
a) Secondary voltage: U2 = ? (V) b) Current in the primary winding: I1 = ? (A) Current in the secondary winding: I2 = ? (A) Hint a)
The part a) can be solved using the relationship between the voltage on the coils of the transformer and the number of turns.
Hint: Transformer, turns ratio
AC voltage can be transformed to another voltage of the same frequency using a transformer. The transformer works on the principle of electromagnetic induction. Two coils are wound on a common core. The primary coil is connected to an AC voltage source. A current flowing in the primary coil generates a time-varying magnetic field in the core. This magnetic field induces AC voltage in the secondary coil. The magnetic field is common for all turns, therefore on each turn of the primary and secondary coil is the same voltage Ut.
The voltage on the primary coil: \(U_1=N_1 U_t\)
The voltage on the secondary coil: \(U_2=N_2 U_t\)
where N1 and N2 is the number of turns of the primary and secondary coil.
Voltage on one turn:
\[U_t=\frac{U_2}{N_2}=\frac{U_1}{N_1}\]Thus:
\[\frac{U_2}{U_1}=\frac{N_2}{N_1}=k\]Number k is called a transformation ratio.
Hint b)
To solve the part b) we use the power of electric current. In an ideal transformer, the power on the primary coil is equal to the power on the secondary coil. We also use Ohm's law.
Analysis
The ratio of the voltage on the coils is the same as a ratio of their turns. This ratio is called the transformation ratio.
If the secondary circuit is open, the voltage on the primary coil is transformed to the voltage on the secondary coil voltage accordingly to the transformation ratio. Secondary voltage is evaluated from the ratio of the number of turns in the coils and the voltage on the primary coil.
Ideally, the power on the secondary coil is equal to the power on the primary coil. The power on the secondary coil is expressed through the voltage on the secondary coil that we have calculated in part a), and a resistance, to which the coil is connected. We compare the power on both coils. We know the voltage on both circuits; therefore we can determine the primary current. The secondary current is determined from Ohm's law.
a) Solution
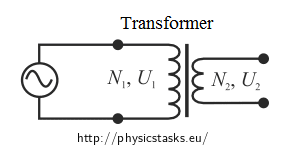
To solve this task we use the fact that the ratio of the voltage on the secondary and on the primary coil is the same as the ratio of the number of turns of both coils:
\[k=\frac{U_2}{U_1}=\frac{N_2}{N_1}\]We evaluate the unknown secondary voltage:
\[U_2=\frac{N_2}{N_1}\,U_1\]
We substitute the given values:
\[U_2=\frac{10}{500}\cdot 120 \,\mathrm V=2.4 \,\mathrm V\]b) Solution
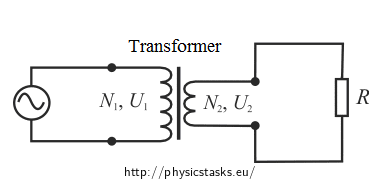
We determine the secondary current using Ohm's law. A resistor of known resistance is connected in the circuit and we have determined the voltage in the previous section:
\[I_2=\frac{U_2}{Z}\]
\[I_2=\frac{U_2}{R}\]
When calculating the primary current, we assume that this is an ideal transformer, i.e. that it is lossless. In this case, for the electric power on the coils it applies:
\[P_1=P_2\]
The electric power P1 is determined as follows
\[P_1=U_1\,I_1\]
The electric power P2 can be expressed as:
\[P_2=U_2 I_2=\frac{(U_2)^2}{R}\]
We substitute into previous relationship and evaluate the primary current:
\[U_1 I_1=\frac{(U_2)^2}{R}\]
\[I_1=\frac{(U_2)^2}{U_1 R}\]
Numerical substitution:
Primary current:
\[I_1=\frac{(2.4)^2}{120 {\cdot} 15}\,\mathrm A=3.2 \,\mathrm mA\]
Secondary current:
\[I_2=\frac{2.4}{15}\,\mathrm A=0.16\,\mathrm A\]
Answer
If the secondary circuit is open, the secondary voltage is 2.4 V.
If the secondary coil is connected to a resistance load, the primary current is 3.2 mA and the secondary current is 0.16 A.
Link to an experiment
An experiment for this problem can be found here: Induced Voltage.




