Conductor Moving in a Magnetic Field
Task number: 1547
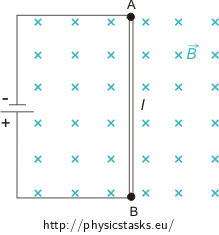
A straight wire 1 m long (in the figure denoted AB) of resistance 2 Ω is placed in a magnetic field with magnetic induction of 0.1 T. The conductor is connected to a voltage source of 1 V.
a) Determine the current I flowing through the conductor, provided that:
- the conductor is at rest,
- the conductor moves at a speed of 4 m·s-1 to the right,
- the conductor moves at a speed of 4 m·s-1 to the left
b) In which direction and how fast do we need to move the conductor, so that the current flowing through the conductor is zero? What direction do we need to move the conductor so that the current flowing through the conductor were the same as the current in the conductor at rest?
Hint
When is an electromotive force induced in the circuit? In what case is it added to the voltage of the source and when is it subtracted?
Analysis a)
A change of magnetic flux through the surface area of the loop shown in the figure induces an electromotive force in the circuit. It can be thought of as the "number of induction lines passing through the area of the loop". It is very important that it does not depend on the total number of the lines passing through the loop area, but only on the change of this number. The size of the electromotive force and induced current depends on the rate of change of this number. Therefore, in the first case (the conductor is stationary) the magnetic field does not affect the circuit. The current can be determined by applying Ohm's law.
In the second case, the conductor is moved at a constant speed to the right, thereby the surface area of the loop increases, and hence the flux through the loop also increases. A current induced in the circuit generates a magnetic field around the conductor. The magnetic induction lines of this field have such a direction as to prevent the change in the magnetic flux (they try to reduce it). Therefore, their direction is opposite to the direction of the external magnetic field, thus pointing toward us. The direction of the induced current is determined with application of Ampere's rule. The thumb indicates the direction of magnetic induction lines and curved fingers show the direction of the current in the conductor. In this case the current flows in the counter clockwise direction. The direction of the induced current and the current from the battery is the same; therefore we can add them together. Similarly we determine the voltage. The overall voltage is given by the sum of the induced electromotive force and battery voltage.
In the third case, the conductor is moved at a constant speed to the left, thereby decreasing the area of the loop and the "number of lines of induction through the loop". A current induced in the circuit generates a magnetic field around the conductor. The induction lines of this field have such a direction as to prevent the change in the magnetic flux (they want to increase it). We determine the direction of the induced current by Ampere's rule. This time the current flows in the clockwise direction. The directions of the induced current and the current from the source are opposite. Therefore, we need to subtract them. We determine the voltage similarly; the total voltage is the difference between the electromotive force and the voltage from the source.
Solution a)
In the first case, no electromotive force is induced. We determine the current from Ohm's law
\[U=R I\hspace{15px}\Rightarrow\hspace{15px}I_{\mathrm{at rest}}=\frac{U}{R}.\]In the second case, the current is also determined from Ohm's law, where the voltage is given by the voltage of the source plus the electromotive force Ui.
\[I_{\mathrm{right}}=\frac{U+U_i}{R}.\]The induced electromotive force is equal to the change in magnetic flux through the loop area per time
\[U_i=\frac{\Delta \Phi}{\Delta t}.\]The flux is determined as follows
\[\Phi =B S \cos \alpha,\]where α is the angle between the normal to the surface of the loop and the inductive lines; in our case α = 0° and cos α = 1. The surface area S is given by
\[S = l v t.\]For the induced voltage we obtain
\[U_i = \frac{\Delta (Blvt)}{\Delta t}.\]All of the variables in the numerator are constants, except for time
\[U_i = \frac{Blv\Delta t}{\Delta t}=Blv.\]We substitute into the formula for electric current
\[I_{\mathrm{right}}=\frac{U+Blv}{R}.\]In the third case we determine the current from Ohm's law. The overall voltage is given by the difference between the voltage of the source and the electromotive force.
\[I_{\mathrm{left}}=\frac{U-U_i}{R}.\]The induced voltage depends on the rate of change of magnetic flux. In both cases, the conductor is moved at the same speed; therefore the size of electromotive force is the same as in the second case
\[I_{\mathrm{left}}=\frac{U-Blv}{R}.\]Given values and numerical insertion a)
\[l = 1\,\mathrm{m}\] \[R=2\,\mathrm{\Omega}\] \[B=0{,}1\,\mathrm{T}\] \[U=1\,\mathrm{V}\] \[I_{\mathrm{rest}}=\mathrm{?} \] \[I_{\mathrm{right}}=\mathrm{?} \] \[I_{\mathrm{left}}=\mathrm{?} \]
\[I_{\mathrm{rest}}=\frac{U}{R}=\frac{1}{2}\,\mathrm{A}=0{.}5\,\mathrm{A}\] \[I_{\mathrm{right}}=\frac{U+U_i}{R}=\frac{U+Blv}{R}=\frac{1+0{.}1{\cdot}1\cdot4}{2}\,\mathrm{A}=0{.}7\,\mathrm{A}\] \[I_{\mathrm{left}}=\frac{U-U_i}{R}=\frac{U-Blv}{R}=\frac{1-0{.}1{\cdot}1\cdot4}{2}\,\mathrm{A}=0{.}3\,\mathrm{A}\]Answer a)
A current flowing through a stationary conductor is 0.5 A.
If the conductor moves at a speed of 4 m·s-1 to the right, the current in the conductor is 0.7 A.
If the conductor moves at a speed of 4 m·s-1 to the left, the current in the conductor is 0.3 A.
Analysis b)
The voltage induced in the circuit must be of the same size as the voltage of the source so that no current flows through the conductor.
Provided that the current flowing through the conductor is the same as the current in the conductor at rest, the magnetic flux through the loop must not change, therefore the "number of lines of induction passing through the loop" must be the same.
Solution b)
We evaluate the current from Ohm's law.
\[I=\frac{U\pm U_i}{R}\]The voltage induced in the circuit must be of the same size as the voltage of the source, so that no current flows through the conductor.
\[U=U_i\]We substitute the relationship derived in the previous section for the electromotive force
\[U=U_i=Bvl.\]We evaluate the unknown speed v
\[v=\frac {U}{Bl}.\]The direction of movement of the loop can be determined from solution a); when moving the conductor to the left, the current decreases, therefore it is close to zero. In this case, the wire moves to the left with velocity v.
If the wire moves at speeds greater than v to the left, the induced voltage is greater than the voltage from the source and the total current in the conductor is negative (in the opposite direction).
Given values and numerical insertion
\[l = 1\,\mathrm{m}\] \[R=2\,\mathrm{\Omega}\] \[B=0.1\,\mathrm{T}\] \[U=1\,\mathrm{V}\] \[I=0 \,\mathrm{A}\] \[v=\mathrm{?} \]
\[v=\frac{U}{Bl}=\frac{1}{0{.}1{\cdot} 1}\,\mathrm{m\,s}^{-1}=10\,\mathrm{m\,s}^{-1}\ \]Answer b)
The conductor must be moved to the left at a speed of 10 m·s-1 so that no current flows through the conductor.
The conductor needs to be moved in the direction of the induction lines so that the current in the moving conductor is the same as the current in the conductor at rest.



