The Length of the Discharge of the Neon Lamp

Task number: 1164

A neon glow lamp is connected to an AC source with an effective voltage of 230 V and a frequency of 50 Hz. The neon glow lamp is connected in series with a 150 kΩ resistor. The striking voltage of the neon glow lamp with the resistor is 116 V, the quenching voltage is 87 V. Determine how long the neon lamp glows during the first half of a period.

Note: The neon glow lamp described in the assignment is a real one which we can actually find e.g. in light switches in the corridors of various buildings.

Notation

From the assignment we know:

Source voltage:	U = 230 V
Source voltage frequency:	f = 50 Hz
Resistor resistance:	R = 150 kΩ
Striking voltage of the neon glow lamp with the resistor:	U_S = 116 V
Quenching voltage of the neon glow lamp with the resistor:	U_Q = 87 V

We want to find out:

How long the neon lamp glows:

Δt = ? (s)

Hint 1 – striking voltage
The neon lamp starts glowing when the voltage reaches the value of the striking voltage U_S = 116 V. It is glowing all the time when the voltage is higher than U_S. When the voltage drops belowU_Q = 87 V, the neon lamp stops glowing.
Hint 2
Remember the time evolution of the alternating harmonic voltage. How are the effective and the maximal voltage related to each other?
Hint 3
Time evolution of the voltage is described by the sine function:
\[u\left(t\right)=U_m \sin{\left(\omega t\right)}\]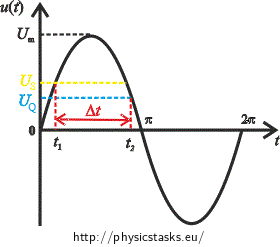
Task analysis
The neon lamp starts glowing when the voltage reaches the value of the striking voltage and it stops glowing when the voltage drops below the quenching voltage. Our task is to find out the time interval between the moment when the voltage reaches the striking voltage and the moment when it drops below the quenching voltage. We use the description of the time evolution of the alternating voltage by the sine function to do this.
Solution

The time evolution of the alternating voltage is described in general by the formula:
\[u(t)=U_m\, \sin(\omega t).\]
For the maximum voltage U_m we have:
\[U_m=\sqrt{2}U\mathrm{,}\]
where U is the effective voltage that is known from the assignment.

1) The striking voltage:

We are looking for the moment when the instantaneous voltage equals the striking voltage of the neon lamp, so we will solve the equation:
\[U_S=U_m\, sin(\omega t_1).\] \[U_S=\sqrt{2}U\, sin(\omega t_1).\]
We express the time when the neon lamp starts glowing as:
\[\sin(\omega t_1)=\frac{U_S}{\sqrt{2} U}\] \[\omega t_1=\mathrm{arcsin} \left(\frac{U_S}{\sqrt{2} U}\right)\] \[t_1=\frac{\mathrm{arcsin} \left(\frac{U_S}{\sqrt{2} U}\right)}{\omega}\]
For the formula
\[\mathrm{arcsin} \left(\frac{U_S}{\sqrt{2} U}\right)\]
we obtain two numerical values:

a)\(\hspace{10px}\mathrm{arcsin} \left(\frac{U_S}{\sqrt{2} U}\right)=\mathrm{arcsin} \left(\frac{116}{\sqrt{2}\cdot 230}\right)=0{,}36\)

b)\(\hspace{10px}\mathrm{arcsin} \left(\frac{U_S}{\sqrt{2} U}\right)=\mathrm{arcsin} \left(\frac{116}{\sqrt{2}\cdot 230}\right)=\pi - 0{,}36=2{,}78\)

We choose the lower value a) because it corresponds to the time t₁ illustrated in the picture.

We numerically evaluate the formula for the time when the neon lamp starts glowing:
\[t_{1}=\frac{\mathrm{arcsin} \left(\frac{U_S}{\sqrt{2} U}\right)}{\omega}=\frac{\mathrm{arcsin} \left(\frac{U_S}{\sqrt{2} U}\right)}{2 \pi f}=\frac{\mathrm{arcsin} \left(\frac{116}{\sqrt{2}\cdot 230}\right)}{2\pi\cdot 50}\,\dot{=}\,1{,}16\,\mathrm {ms}\]

Note: If your numerical result is different from the result above, check if your calculator is set to radians. If you want to use degrees for your calculation, it is necessary to divide the time expressions by the value of 360°instead of 2π.

2) The quenching voltage:

We are looking for the moment when the instantaneous voltage equals the quenching voltage of the neon lamp, so we will solve the equation:
\[U_{Q}= U_m \, \sin(\omega t_2)\] \[U_{Q}=\sqrt{2} U \, \sin( \omega t_2)\]
We express the time when the neon lamp stops glowing:
\[\sin(\omega t_2)=\frac{U_{Q}}{\sqrt{2} U}\] \[\omega t_2=\mathrm{arcsin} \left(\frac{U_{Q}}{\sqrt{2} U}\right)\] \[t_2=\frac{\mathrm{arcsin} \left(\frac{U_{Q}}{\sqrt{2} U}\right)}{\omega}\]
For the formula \[\mathrm{arcsin} \left(\frac{U_{Q}}{\sqrt{2} U}\right)\] we obtain two numerical values:

a)\(\hspace{10px}\mathrm{arcsin} \left(\frac{U_{Q}}{\sqrt{2} U}\right)=\mathrm{arcsin} \left(\frac{87}{\sqrt{2}\cdot 230}\right)=0{,}27\)

b)\(\hspace{10px}\mathrm{arcsin} \left(\frac{U_{Q}}{\sqrt{2} U}\right)=\mathrm{arcsin} \left(\frac{87}{\sqrt{2}\cdot 230}\right)=\pi - 0{,}27=2{,}87\)

We choose the larger value b) because it corresponds to the time t₂ illustrated in the picture.

We numerically evaluate the formula for the time when the neon lamp stops glowing:
\[t_{2}=\frac{\mathrm{arcsin} \left(\frac{U_{Q}}{\sqrt{2} U}\right)}{\omega}=\frac{\mathrm{arcsin} \left(\frac{U_{Q}}{\sqrt{2} U}\right)}{2 \pi f}=\frac{\mathrm{arcsin} \left(\frac{87}{\sqrt{2}\cdot 230}\right)}{2 \pi\cdot 50}\dot{=}\, 9{,}14\,\mathrm {ms}\]

We obtain the time interval during which the neon lamp glows by subtracting the time values that we calculated from the sine function argument amplitude for particular voltages.
\[ \Delta t = t_2 - t_1 = (9{,}14-1{,}16)\, \mathrm{ms} \,\dot{=}\,8\, \mathrm{ms} \]
Answer
The time interval in which the neon lamp glows during one half of the alternating voltage period is: \[ \Delta t=8\,\mathrm{ms} \]
Comment
We have solved the task for the first half of the alternating voltage period only. During the whole period the neon lamp “flickers” twice because it glows with either direction of the current.