Instantaneous Voltage and Current Values in a Series RLC Circuit
Task number: 1543
An AC series circuit consists of a resistor with resistance of 90 Ω, a coil with inductance of 1.3 H and a capacitor with capacitance of 10 μF. The circuit is connected to an AC voltage source with amplitude of 100 V and frequency of 50 Hz. Write an equation for instantaneous values of voltage and current in the circuit, if the initial phase of the current is zero.
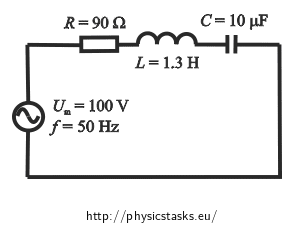
Given values
We write down the quantities and values given in the section Assignment
Amplitude of the alternating voltage in the circuit Um = 100 V Frequency of the AC power source f = 50 Hz Resistance of the resistor R = 90 Ω Inductance of the coil L = 1.3 H Capacitance of the capacitor C = 10 μF Initial current phase φ0i = 0 Quantities we want to determine:
Instantaneous current value i(t) = ? (A) Instantaneous voltage value u(t) = ? (V) Hint 1
The behaviour of alternating voltage and current can be described by a sine function.
Find the equations describing the instantaneous values of the alternating voltage and the current.
Hint 2
When evaluating these equations we need to know the current amplitude Im and a phase difference φ0u between the voltage and the current. These we determine by using Ohm's law for alternating current.
In the task Series RLC Circuit you can find a detailed explanation of the calculation of the current and the phase difference.
Determining amplitude of current Im
We apply Ohm's law for a circuit with alternating current:
\[I_m=\frac{U_m}{Z}=\frac{U_m}{\sqrt{R^2+\left(X_L-X_C\right)^2}}=\frac{U_m}{\sqrt{R^2+\left(2 \pi f L - \frac{1}{2 \pi f C}\right)^2}} \]
We insert the given values:
\[I_m=\frac{100}{\sqrt{90^2+\left(2 \pi \cdot 50 {\cdot} 1{.}3 - \frac{1}{2 \pi \cdot 50 {\cdot} 10 \cdot 10^{-6}}\right)^2}} \, \mathrm{A} \] \[I_m \,\dot{=}\, 0{.}79 \, \mathrm{A}\]Determining phase difference between voltage and current φ0u
We use the formula for phase difference expressed by impedance of each element.
\[ \mathrm{tg\,} \varphi_{0u} = \frac{X_L - X_C}{R}= \frac{\omega L- \frac{1}{ \omega C}}{R}= \frac{2 \pi f L- \frac{1}{ 2 \pi f C}}{R} \] \[\varphi_{0u} = \mathrm{arctg\,}\left(\frac{2 \pi f L- \frac{1}{ 2 \pi f C}}{R}\right)\]
Numerical solution:
\[\varphi_{0u} = \mathrm{arctg\,}\left(\frac{2 \pi f L- \frac{1}{ 2 \pi f C}}{R}\right)= \mathrm{arctg\,}\left(\frac{2\pi \cdot 50 {\cdot} 1.3 - \frac{1}{ 2 \pi \cdot 50 {\cdot} 10 \cdot 10^{-6}}}{90}\right)\] \[\varphi_{0u} \,\dot{=}\, 45 ^{\circ} = \frac{\pi}{4} \]Instantaneous values of alternating voltage and current
Instantaneous value of alternating current:
The phase difference of the current is zero; the current amplitude Im has been calculated above.
\[ i(t)=I_m \, \sin(\omega t + \varphi_{0i})=I_m\, \sin( 2 \pi f t + \varphi_{0i} ) \] \[ i(t)\,\dot{=}\,0.79 \cdot \sin(2 \pi 50 t)\,\mathrm A =0.79 \cdot \sin(100 \pi t)\,\mathrm A\]
Instantaneous value of alternating voltage:We know the voltage amplitude Um and we have determined the phase difference.
\[ u(t)=U_m \, \sin(\omega t + \varphi_{0u})=U_m \, \sin( 2 \pi f t + \varphi_{0u} ) \] \[u(t)\,\dot{=}\,100 \cdot \sin( 2 \pi 50 t + \frac{\pi}{4} )\,\mathrm V = 100\cdot \sin( 100 \pi t + \frac{\pi}{4} )\,\mathrm V\]The time values inserted into the equations are converted into seconds.
Answer
The equations for instantaneous values of the voltage and the current in a series RLC circuit with AC have approximately the shape of:
\[ i(t)=0{.}79 \cdot \sin\left({100 \pi t}\right)\,\mathrm A\] \[u(t)=100 \cdot \sin\left( 100 \pi t + \frac{\pi}{4} \right)\,\mathrm V \]




