Inductance of a Coil Rotating in a Magnetic Field
Task number: 1542
A cylindrical coil 10 cm long and with 600 turns and a radius of 2 cm rotates in a magnetic field with magnetic induction of 3·10-3 T. Determine:
a) the maximum induction flux inside the coil,
b) the inductance of the coil.
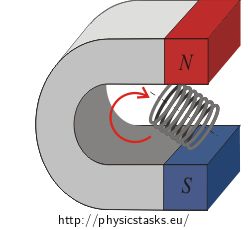
Hint a) Maximum value of magnetic flux
Magnetic flux through a coil is at maximum, when the number of magnetic lines of induction passing through the coil is at maximum.
Realize how we need to place the coil against the vector of magnetic induction to reach the maximum flux through the coil.
Help b) What is inductance of a coil
Inductance of a coil is a scalar quantity that characterizes a self-induction of a closed conductor, e.g. a coil. A closed conductor with electric current I induces a magnetic field around itself, for which we can determine the magnetic flux Φ through the conductor. The inductance of the conductor is then given by
\[L=\frac{\Phi}{I}.\]The magnetic field is proportional to the electric current in the conductor and the magnetic flux is proportional to the magnetic field. Therefore, the inductance does not depend on electric current. Its value is given only by the shape and the arrangement of the conductor.
The unit of inductance is henry – denoted H.
Analysis
Maximum flux through the coil
The magnetic flux through the coil is at maximum, when the number of induction lines passing through the coil is at maximum. This occurs when the vector of magnetic induction is perpendicular to the surface of the coil loop.Inductance of the coil
As the coil rotates in the magnetic field, the induction flux through the coil changes and a time–varying current is induced in the coil. If an electric current passes through a coil, it generates a magnetic field around the coil. The magnetic flux of this field is proportional to the induced current. The constant of proportionality between the magnetic induction flux through the coil and the induced current is called inductance.
Solution a) Maximum flux through the coil
We express a relationship for the magnetic flux through the coil. Giving the fact that we can consider the magnetic field, in which the coil is placed, to be uniform, the magnetic flux Φ through the coil is given by
\[\Phi=NBS\,cos\alpha,\]where α is the angle between the vector of magnetic induction \(\vec{B}\) and the normal vector of the surface \(\vec{S}\).
The magnetic flux through the coil is at maximum when cos α = 1, i.e. α = 0°. Therefore, the vectors \(\vec{B}\) and \(\vec{S}\)are parallel, which means that the vector of magnetic induction \(\vec{B}\) is perpendicular to the plane of the turn S. The maximum flux through the coil is then
\[\Phi_{max}=NBS.\]The surface area of one turn S equals the surface area of a circle with radius r.
For maximum flux Φmax through the coil it applies
\[\Phi_{max}=\pi r^2 NB.\]Solution b) Inductance of a coil
A rotating coil is placed in a magnetic field and a therefore a voltage is induced in the coil. If the coil is connected, also electric current can be induced. This current creates additional induced magnetic field, we call it the field of the coil. Inductance L is the constant of proportionality between the instantaneous magnetic flux through the coil Φ and the immediate current i which passes through the coil, i.e.
\[\Phi(t)=Li(t).\tag{1}\]We consider the coil to be placed in such a position that the magnetic flux is at maximum. In the previous section we have derived that the flux is maximum, when the vector of the magnetic induction is perpendicular to the surface of the coil.
For the magnetic flux it applies
\[\Phi=NBS.\]For B we substitute the magnetic induction inside a long coil
\[B=\mu_o\frac{N}{l}i.\]We substitute the partial relations into the equation (1)
\[NBS=Li,\] \[N\mu_o\frac{N}{l}iS=Li\]and evaluate the inductance of the coil L
\[L=\mu_o\frac{N^2S}{l}.\]Given values and numerical substitution
\[l\,=\,10\,\mathrm{cm}=\,0.10\,\mathrm{m}\] \[r\,=\,2\,\mathrm{cm}=\,0.02\,\mathrm{m}\] \[B\,=\,3{\cdot}10^{-3}\,\mathrm{T}\] \[N\,=\,600\] \[\Phi\,= \,?\] \[L\,= \,?\]From The Handbook of Chemistry and Physics
\[\mu_o\,= \,4\pi\cdot10^{-7}\,\mathrm{Hm^{-1}}\]
\[\Phi_{max}=\pi r^2 NB=\pi\cdot0.02^2{\cdot}600\cdot 3{\cdot}10^{-3}\,\mathrm{Wb}\dot{=}2{\cdot}10^{-3}\,\mathrm{Wb}\] \[L=\mu_o\pi\,\frac{(Nr)^2}{l}=4\cdot\pi^2{\cdot}10^{-7}\cdot\frac{(600{\cdot}0.02)^2}{0.10}\,\mathrm{H}\dot{=}6{\cdot}10^{-3}\,\mathrm{H}\]Answer
The maximum flux passing through the coil is approximately Φ = 2 mWb.
The coil inductance is approximately L = 6 mH.




