Electron in an Accelerator
Task number: 1550
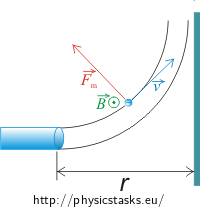
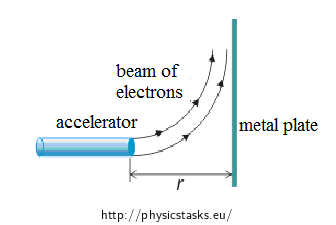
Electrons with kinetic energy Ek fly out of an accelerator. A metal plate is placed in the distance r from the accelerator; the plate is perpendicular to the beam of electrons leaving the accelerator. (See figure below). Prove that we can prevent the beam hitting the plate by diverting the beam with a magnetic field \(\vec{B}\) with size
\[B=\sqrt{\frac{2mE_k}{e^{2}r^{2}}},\]where m and e are the electron mass and size of the electron charge. What is the orientation of the vector of magnetic induction?
Hint
The beam of electrons is diverted by a magnetic force, which is perpendicular to the direction of movement, and thus acts as a centripetal force.
Analysis
Without the presence of magnetic field, the electrons leaving the accelerator move linearly and uniformly and hit the metal plate. If we want to prevent the beam colliding with the plate, we need to divert the electrons from their original direction.
The beam of electrons is diverted by passing through a magnetic field. A magnetic force acts on charged particles (beam of particles) moving in a magnetic field. The force is perpendicular to the direction of the moving particles, thus acts as a centripetal force and curves the trajectory of the particles. Particles in a magnetic field move along a circle.
We determine the size of magnetic induction from the relation for magnetic and centripetal force and compare it with the given relationship.
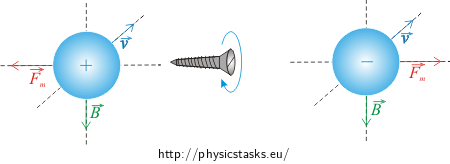
When determining the direction of the magnetic induction vector, we utilize this knowledge: If the velocity vector is perpendicular to the vector of magnetic induction, then the force acting on the particle is at maximum and the vector is perpendicular to the vector of magnetic induction. In this task this means that the vector of magnetic induction is perpendicular to the plane of the figure (see the figure in the next section). Now we just need to determine whether it is oriented out of or into the plane of the figure. We determine the orientation by Fleming's left-hand rule, or the clockwise screw rule.
Solution
Consider that a particle with a charge e moves in a magnetic field of the magnetic induction \(\vec{B}\) with a velocity v. It is convenient that the vector of velocity is perpendicular to the vector of magnetic induction, then the magnetic force \(\vec{F}_m\) acting on the particle is at maximum and its size is given by
\[F_m = evB.\]The magnetic force \(\vec{F}_m\) acts perpendicularly to the direction of movement, thus as a centripetal force. As a result, the particle in the magnetic field moves along a circle. For the size of the centripetal force the relation
\[F_c=m\frac{v^2}{r}.\]applies.
We compare both relations for the forces
\[F_m=F_c,\] \[evB=\frac{mv^2}{r}\]and evaluate the magnetic induction B
\[B=\frac{mv}{re}.\]Since we do not know the velocity of the electrons v, we evaluate it from the given kinetic energy Ek
\[E_k=\frac{1}{2} mv^2\hspace{15px}\Rightarrow \hspace{15px} v=\sqrt{\frac{2E_k}{m}}.\]We adjust the relation and substitute it into the relation for magnetic induction B
\[B=\frac{m}{re}\sqrt{\frac{2E_k}{m}}.\]After adjusting we obtain an expression which is consistent with the expression in the assignment
\[B=\sqrt{\frac{2mE_k}{r^2e^2}}.\]Determining the direction of magnetic induction B
The orientation of magnetic field can be determined by:
1) Fleming's left-hand rule
Outstretched fingers point in the direction of the current in a conductor and magnetic field lines (or vector the \(\vec{B}\))enter the palm, thumb shows the direction and orientation of a magnetic force \(\vec{F}_m\), which acts on the conductor.
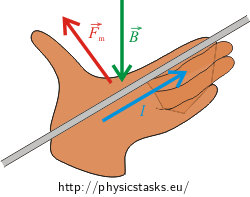
The direction of electric current in the conductor is the direction of motion of positive particles. In our case we examine a motion of electrons, which are negative particles. Therefore, the left-hand fingers point in the opposite direction to the direction of the moving electrons. According to the figure in the assignment, the electrons are diverted upward; therefore the magnetic force acts upward. The vector of magnetic induction must therefore point out of the plane of the figure.
2) Clockwise screw rule
If we rotate the screw clockwise from the direction of the velocity vector \(\vec{v}\) to the direction of the magnetic field \(\vec{B}\) (by an angle smaller than \(\pi\)), the screw bores in the direction of the force \(\vec{F}_m\) acting on a positive charge. If the charge is a negative direction of the force \(\vec{F}_m\) is opposite.
Applying this rule, we obtain the same direction of the magnetic induction \(\vec{B}\) as above.
Given values and numerical substitution
\(E_k=5\,\mathrm{keV}\) - Electron accelerated by a voltage of 5000 VWe substitute the energy with the unit joule into the derived relation.
\[E_k=8{\cdot} 10^{-16}\,\mathrm{J}\] \[r=5\,\mathrm{mm}=5 {\cdot} 10^{-3}\,\mathrm{m}\]From The Handbook of Chemistry ad Physics:
\[m_e=9.1 {\cdot} 10^{-31}\,\mathrm{kg}\] \[e=1.6{\cdot} 10^{-19}\,\mathrm{C}\]
\[B=\sqrt{\frac{2mE_k}{e^{2}r^{2}}}=\sqrt{\frac{2{\cdot} 9.1{\cdot} 10^{-31}\cdot8{\cdot} 10^{-16}}{\left(1.6{\cdot} 10^{-19}\right)^{2}\left(5 {\cdot} 10^{-3}\right)^{2}}}\,\,\,\mathrm{T}\,\dot{=}\,0{.}048\,\mathrm{T}\] \[B\,\dot{=}\,48\,\mathrm{mT}\]Answer
We have proved that we can prevent the beam hitting the plate, if the beam of electrons is diverted by a magnetic field of size
\[B=\sqrt{\frac{2mE_k}{e^{2}r^{2}}}.\]For the given values, the size of the magnetic field is approximately
\[B\,\dot{=}\,48\,\mathrm{mT}.\]The direction of magnetic field is out of the plane of the figure.
Comment
From the cylindrical symmetry of the task it is evident that any orientation of the magnetic field perpendicular to the electron beam is suitable.
In our task we chose one the direction of electron beam and that the electrons are deflected upward. Therefore the magnetic induction diverting the beam points out of the plane of the figure.