Cyclotron
Task number: 551
Deuterons, the nucleuses of heavy hydrogen, are accelerated in a cyclotron. Determine the frequency of the voltage source, if the value of magnetic field strength in the cyclotron makes 1.5 T and the mass of deuterons is 3.3·10-27 kg.
Determine the cyclotron radius for particles, which leave the cyclotron with a kinetic energy of 16 MeV.
How many times does the deuteron cross between “D” electrodes (also called “dees”), if the electrical potential difference between the two dees is 50 kV?
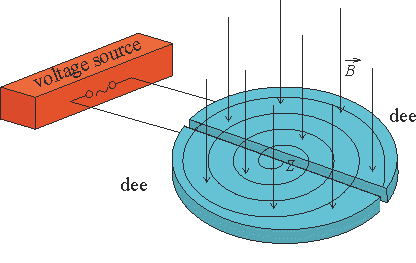
The principle of the cyclotron
A cyclotron is a type of particle accelerator. Cyclotrons accelerate charged particles to increase their kinetic energy. These high-energy particles are also used e.g. in nuclear research or in hospitals to obtain radioactive preparations for medical and diagnostic purposes.
The cyclotron is made up of two semi cylinder’s conductors that are opened on the straight side. These D-shaped conductors are made of a non-ferromagnetic material (e.g. sheet copper) and are called “dees”. The dees are placed in a homogenous magnetic field with a great magnetic induction that is perpendicular to the conductors. An alternating voltage is brought into a narrow gap between the conductors. If a charged particle enters the electric field between dees near the center of the cyclotron, it is accelerated and gains a velocity that runs perpendicularly to the magnetic field inside of one of the dees.
The magnetic field forces the particles to travel in a spiral path. The energy is applied to the particles as they cross the gap between dees in the cyclotron and so the particles are accelerated. This effect increases the radius of the circle and so the path is spiral (see figure in the assignment). With no change of energy the charged particles will follow a circular path. The bigger speed of particles means a bigger radius of the path. The high-speed particles get of the cyclotron in the moment when the radius of the path reaches the radius of the cyclotron.
The trick of the cyclotron lies in accelerating of the particles alongside with increasing of the length of the path (semicircle) therefore the flight time of the particles around the circle remains constant (this is derived in detail in the problem solution). On that account it is sufficient to connect a field with a constant frequency between dees. The particles will be accelerated in the right direction and it is not necessary to change the frequency of the electric field (time interval between the voltage pulses) by accelerating of the particles.
Analysis
A deuteron (positively charged particle) flies out of the source Z in the center of the cyclotron and it is initially moving to the negatively charged D-shaped conductor (so-called „dee“). The motion of the particle is accelerated. The electric field has no effect on the deuteron after reaching the dee, because the space inside the dee screens out the electric field. But the dees do not screen out the magnetic field and therefore the deuteron is moving in a circular path. The radius of the circle depends on the speed of the particle.
Meanwhile the deuteron flies inside into the negatively charged dee, the voltage between the two dees changed its polarity. The “D” electrode in front of the particle is negatively charged again and the particle will be accelerated then. This process continues and the deuteron flies in a spiral path. The deuteron flies out of the cyclotron after reaching the edge of the dee.
The cyclotron accelerates the deuteron successfully, if the frequency f that the deuteron has to run in the magnetic field, is equal to the frequency fs of the electric source.
Now we are interested in how many times the positive charged particle runs between the D-electrodes in the accelerator to obtain the required energy. It is important to realize that the kinetic energy of the particle is negligible when it comes into the center of the cyclotron. The particle obtains energy proportionate to the voltage between dees during every single acceleration of the particle.
Solution a)
Deuterons with the charge e enter the homogenous magnetic field with the magnetic induction \(\vec{B}\) and the velocity \(\vec{v}\) (the velocity is perpendicular to the magnetic induction). The size of the magnetic force \(\vec{F}_m\) that interacts with the particle is equal to:
\[F_m=evB.\]The size of the centripetal force F during the uniform movement round the circle is formulated:
\[F=ma=\frac{mv^2}{r}.\]The magnetic force is the centripetal force in this case and therefore:
\[evB=\frac{mv^2}{r}.\]The radius of the circle that the particle moves around is:
\[r=\frac{mv}{eB}.\tag{1}\]The time to run around the semicircle (one half of the period) \(\frac{T}{2}\) is equal to the circumference of the circle πr divided by the velocity v of the particle:
\[\frac{T}{2}=\frac{\pi r}{v}=\frac{\pi}{v}\frac{mv} {eB}=\frac{\pi m}{eB}.\]The circulation period T of the particle does not depend on its velocity and its energy. Therefore the time between two flights of the particle past the dees is still equal during the acceleration.
The equation for the frequency f is then:
\[f=\frac{1}{T}=\frac{eB}{2\pi m}.\]The frequency f of the circulation of the particle in the magnetic field has to be equal to the frequency of the electric source fz:
\[f_{z}=f=\frac{eB}{2\pi m}.\]The charge e is always constant. The mass m of the particle is constant as well in the nonrelativistic case (just as in our case). The voltage source works with one fixed frequency fz. The cyclotron is then tuned only by changes in the magnetic field, until the bundle of accelerating protons appears.
Solution b)
Consider that the deuteron had negligibly small (almost zero) kinetic energy at the beginning. The kinetic energy Ek that the particle with the charge e gains during the acceleration by the voltage U is equal to:
\[E_k=eU.\]The deuteron has to get through the dees n-times to reach the required energy Emax
\[E_\mathrm{max}=nE_k.\]The number of the runs of the deuteron between dees is:
\[n=\frac{E_\mathrm{max}}{E_k}=\frac{E_\mathrm{max}}{Ue}.\]The radius R of the dees corresponds to the radius of a circle Rmax when the particle has the maximal energy. The size of the cyclotron can be expressed from the relation (1) – the relation for the radius of the circle from the last section:
\[R_\mathrm{max}=\frac{mv}{eB}.\]If the deuteron has the maximal energy, the velocity of the particle will be:
\[E_\mathrm{max}=\frac{1}{2}mv^2\,\,\,\,\Rightarrow\,\,\,\, v=\sqrt{\frac{2E_\mathrm{max}}{m}}.\]The radius of the dee Rmax is:
\[R_\mathrm{max}=\frac{\sqrt{2mE_\mathrm{max}}}{eB}.\]Numerical values
\[e \dot{=} 1.6{\cdot} 10^{-19}\,\mathrm{C}\] \[m \dot{=} 3.3 {\cdot} 10^{-27}\,\mathrm{kg}\] \[B=1.5\,\mathrm{T}\] \[U = 50\,\mathrm{kV}\] \[E_\mathrm{max} = 16\,\mathrm{MeV}\dot{=}2.56{\cdot} 10^{-12}\,\mathrm{J}\] \[f_{z} = ?\] \[n=?\]
\[f_{z}=\frac{eB}{2\pi m}=\frac{1.6{\cdot} 10^{-19}\cdot 1.5}{2\pi\cdot3.3 {\cdot} 10^{-27}}\dot{=} 11 {\cdot} 10^{6}\,\mathrm{s^{-1}}\] \[n=\frac{E_\mathrm{max}}{Ue}=\frac{2.56{\cdot} 10^{-12}}{50{\cdot} 10^{3}\cdot1.6{\cdot} 10^{-19}}=320\] \[R=\frac{\sqrt{2E_\mathrm{max}m}}{eB}=\frac{\sqrt{2{\cdot} 2.56{\cdot} 10^{-12}\cdot 3.3 {\cdot} 10^{-27}}}{1.6{\cdot} 10^{-19}\cdot 1.5}\,\mathrm{m}\,\dot{=}\,0.54\,\mathrm{m}=54\,\mathrm{cm}\]Answer
The cyclotron frequency is approximately 11·106 s-1. The deuteron runs between the D-shaped conductors for 320 times before it reaches the required energy. The radius of the cyclotron equals the radius of the particle with the required energy. The radius is approximately 54 cm.




