Collection of Solved Problems in Physics

Two balls on a thread immersed in benzene

Task number: 281

• Hint 1

  What forces act on the balls and what must they fulfill?

  Draw a figure (free body diagram).

• Hint 2

  Which forces will be changed by dipping the balls into benzene? Will some new forces emerge?

• Figure

  

  

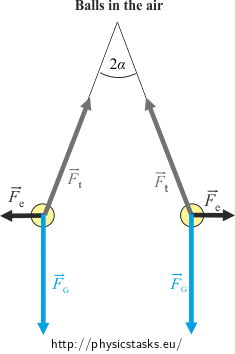
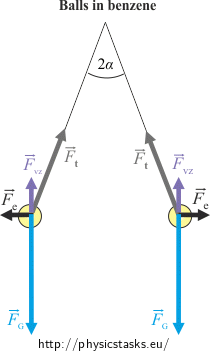
• Analysis

  There are three forces acting on each ball in the air: the weight, the tensile force from the thread and the repulsive electric force. Both balls are stationary thus the net force of these three forces must be zero.

  If the balls are dipped into benzene some of the acting forces will be changed but the net force must remain zero.

  The repulsive electric force will be ε_r-times smaller and the tensile force will be changed as well. The weight stays the same. A new force, the buoyant force, appears.

  In each case we can express the tangent function of the angle α from a right-angled triangle. Comparing both expressions we obtain the unknown density.

  

  

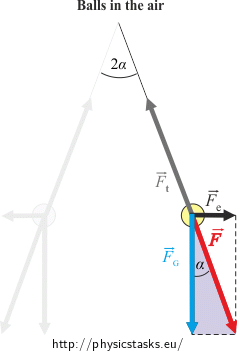
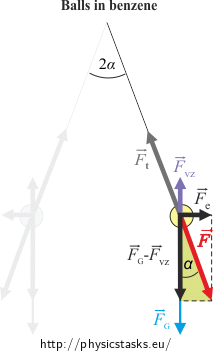
• Solution

  The weight \(\vec{F}_G\) and the tensile force from the thread \(\vec{F}_t\) act on each ball in the air.

  The balls are charged thus they repeal each other by the electric force \(\vec{F}_e\).

  For the magnitude of these forces it holds:

  \[F_G\,=\,mg\] \[F_e\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{Q^2}{r^2}\,,\]

  where r is the distance between the balls.

  The balls are stationary thus the net force of these three forces must be zero.

  We can express the tangent function of the angle α from the “purple “ right-angled triangle:

  \[\mathrm{tg} \alpha=\frac{F_e}{F_G}\,=\,\frac{\frac{1}{4 \pi \varepsilon_0}\, \frac{Q^2}{r^2}}{mg}\] \[\mathrm{tg} \alpha\,=\,\frac{1}{4 \pi \varepsilon_0} \,\frac{Q^2}{mgr^2}\tag{*}\]

  If we immerse the balls into benzene a new force, the buoyant force \(\vec{F}_{VZ}\), appears.

  The weight stays the same but the repulsive electric force \(\vec{F}_e\) will be ε_r-times smaller. The tensile force will be changed as well.

  \[F_G\,=\,mg\] \[F_e\,=\,\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\, \frac{Q^2}{r^2} \] \[F_{VZ}\,=\,V \varrho_b g\]

  The net force of these four forces must remain zero.

  This time we express the tg α from the “green“ right-angled triangle:

  \[\mathrm{tg} \alpha\,=\,\frac{F_e}{F_G-F_{VZ}}\,=\,\frac{\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\, \frac{Q^2}{r^2}}{mg-V \varrho_b g} \] \[\mathrm{tg} \alpha\,=\,\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\, \frac{Q^2}{r^2\left(mg-V \varrho_b g \right)}\tag{**}\]

  Now we compare the expressions (*) and (**) for the tangent function of the angle α:

  \[\frac{1}{4 \pi \varepsilon_0} \,\frac{Q^2}{mgr^2} \,=\,\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\, \frac{Q^2}{r^2g\left(m-V \varrho_b \right)}\]

  We multiply both sides of the equation by \[4 \pi \varepsilon_0 gr^2\] and divide them by Q²

  \[\frac{1}{m} \,=\,\frac{1}{ \varepsilon_r}\, \frac{1}{m-V \varrho_b }\]

  For the mass of one ball m we insert m = V ρ and obtain:

  \[\frac{1}{V\varrho}\, =\,\frac{1}{ \varepsilon_r}\, \frac{1}{V\varrho-V \varrho_b }\]

  From this equation we express the unknown density of the ball ρ as

  \[\frac{1}{\varrho}\,=\,\frac{1}{ \varepsilon_r}\, \frac{1}{\varrho-\varrho_b }\] \[\varrho\,=\,\varepsilon_r \left(\varrho-\varrho_b \right)\]

  We multiply the expression in the brackets by ε_r and move the terms containing the unknown ρ to the left-hand side.

  \[\varepsilon_r \varrho-\varrho\,=\,\varepsilon_r \varrho_b\] \[\varrho \left(\varepsilon_r -1\right)\,=\,\varepsilon_r \varrho_b\] \[\varrho\,=\,\frac{\varrho_b \varepsilon_r }{\varepsilon_r -1}\]

• Numerical values

  ρ_b = 879 kg m^-3.......the density of benzene

  ε_r = 2.3

  ρ = ?  ( kg m^-3)

  ---

  \[\varrho\,=\,\frac{\varrho_b \varepsilon_r }{\varepsilon_r -1}\,=\,\frac{2.3 \,\cdot\, 879}{2.3-1}\,\mathrm{kg\,m^{-3}}\dot\,=\,1 600\,\mathrm{kg\,m^{-3}}\]

  Looking to the tables of material constants we find out that the balls are probably made of some kind of a plastic.

• Answer

  The balls are made of a material with the density \[\varrho=\frac{\varrho_b \varepsilon_r }{\varepsilon_r -1}\dot=1 600\,\mathrm{kg\,m^{-3}}\] .