Electric Eel
Task number: 282
The electric eel (Electrophorus electricus), lives in rivers of South America. It lives on fish which kills by electric shocks. The electric eel generates the voltage in special sets of cells called electroplaques.
The body of the electric eel contains approximately 700 000 electroplaques. We can imagine the electroplaque as an electric source with a voltage Ue = 0.15 V and with an internal resistance Re = 0.25 Ω. Consider the water around the eel as having a resistance Rv = 800 Ω.
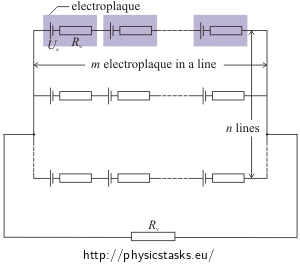
a) Let us assume that the electoplaques are arranged in a rectangle of n lines and there are m electroplaques in each line. Find n and m so that the current through the water from the eel’s head to its tail is maximal.
b) How big would that current be?
Hint 1
Find out how to calculate the voltage across, the current through and the resistance of resistors connected in parallel and in series.
Hint 2
Look up how to find the maximum of a function via derivative.
Image
Let us draw a general scheme of the connection of the electroplaques:
n . . . the number of lines connected in parallel m . . . the number of electroplaques connected in series in one branch N = n·m . . . the number of all electroplaques Ue . . . the voltage across one electroplaque Re . . . the internal resistance of one electroplaque Rv . . . the resistance of water surrounding the eel Analysis – the maximum of a function
The extrema (minimum or maximum) of a function f(x) are located at stationary points or at points that are not differentiable.
The stationary points of function f(x) are points a at which the first derivative is equal to zero:
\[f^, \left(a\right)\,=\,0 \]Analysis – solution
To find the total current through the water around the eel we use the Ohm’s law. Let us express the total voltage and total resistance and thus obtain the expression for the total current as a function of the number of the electroplaques in one line.
The number of electroplaques in one line by which is the current through the water from the eel’s head to its tail maximal is determined by a derivative. The obtained value we insert further into the general equation for the total current. The result yields the maximum of the current we are looking for.
Solution part 1 – the general equation for the total current
We determine the total current through the water from the Ohm’s law:
\[I_{total}\,=\,\frac{U_{total}}{R_{total}}\]For resistors connected in parallel it holds that the voltage on each resistor is the same. For resistors connected in series the voltages are summed. The total voltage across the eel is:
\[U_{total}\,=\,m U_e\]The total resistance is a sum of the resistance of water Rv and the resistance of the eel R.
The resistance of the electroplaques in one line is: \(R_r\,=\,m R_e\)
And for the resistance of the eel R it holds (for n electroplaques connected in parallel):
\[\frac{1}{R}\,=\,\frac{n}{R_r}\,=\,\frac{n}{mR_e}\,\Rightarrow\,R\,=\,\frac{m}{n}R_e\,.\]The total resistance of the circuit \(R_{total}\,=\,R_v+R\,=\,R_v+\frac{m}{n}R_e\).
Now we can express the total current Itotal:
\[I_{total}\,=\,\frac{U_{total}}{R_{total}}\,=\,\frac{m U_e}{\frac{m}{n}R_e+R_v} \,=\, \frac{n m U_e}{mR_e+nR_v}\]As \(n m \,=\, N \), a thus \(n\,=\, \frac{N}{m}\) and we further write:
\[I_{total}\,=\,\frac{NU_e}{mR_e+\frac{NR_v}{m}}\]That is a relation for the total current Itotal where m is the only one variable.
Solution part 2 – the size of m for the maximal current
We already know that the current through water from the eel’s head to its tail is
\[I_{total}\,=\,\frac{NU_e}{mR_e+\frac{NR_v}{m}}\]Now we have to find m for which the total current Itotal is maximal. As the nominator of the previous fraction is constant (is independent ofm), the whole fraction will be maximal if the denominator is minimal.
The sought after value can be find by derivation of the denominator by m:
\[\frac{d}{dm}\left(mR_e+\frac{NR_v}{m}\right)\,=\,R_e+NR_v\left(-\frac{1}{m^2}\right) \,=\,R_e-\frac{NR_v}{m^2}\,,\]and by setting the result to zero
\[R_e-\frac{NR_v}{m^2}\,=\,0\]We express m:
\[m^2R_e-NR_v\,=\,0\] \[{m}^2R_e\,=\,NR_v\]\(m\,=\,\pm \sqrt{\frac{R_v}{R_e}N}\), the negative value of m: does not bear physical meaning.
The current is maximal if:
\[m\,=\,\sqrt{\frac{R_v}{R_e}N}\]Solution part 3 – the numerical insertion
Part a)
For the electroplaques connected in series in one line it holds:
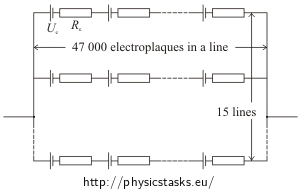
\[m\,=\,\sqrt{\frac{R_v}{R_e}N}\] \[m\,=\,\sqrt{\frac{800}{0{,}25}\cdot 700\,000}\,\dot{=}\,47\,000 \]For n it holds:
\[n\,=\,\frac{N}{m}\,=\,\frac{700\,000}{47\,000}\] \[n\,\dot{=}\,15\]Part b)
The maximal current we find by inserting the obtained m into the expression we have find at the first part of the solution:
\[I_{total} \,=\, \frac{NU_e}{mR_e+\frac{NR_v}{m}}\]Hence:
\[I_{max}\,=\,\frac{700\,000\,\cdot \,0.15}{47\,000\,\cdot \,0.25 + \frac{700\,000\,\cdot \,800}{47\,000}}\, \mathrm{A}\] \[I_{max}\,\dot{=}\,4.4\,\mathrm{A}\]Answer
a) For the current through the water to be maximal the circuit must contain 15 parallel branches. Each branch must contain approximately 47 000 electroplaques connected in series.
b) The total current through water surrounding the electric eel in this connection is 4.4 A.
How is it in reality?
In reality it is a little bit different.
The electroplques are arranged in lines along the electric eel’s body. Each line contains only 5 000 to 6 000 electroplques that are connected in series. The electric eel can produce the voltage across its body approximately 600 V and the current through the surrounding water can be as high as one Ampere.
How is it possible that the electric eel does not harm or kill itself?
It is because the current through each line of electroplques is small, approximately by about two orders smaller than the current through the surrounding water. Moreover the eel’s body is protected by thick skin.
Only if the eel is injured it can kill itself by the electric current.
A summary of rules for computing derivatives of certain combinations of functions
Simple derivatives of some simple functions follow:
Function Derivative \[f\left(x\right)\,=\,c\]
c is a constant \[f^,\left(x\right)\,=\,0\]
\[f\left(x\right)\,=\,cx\]
c is a constant \[f^,\left(x\right)\,=\,c\]
\[f\left(x\right)\,=\,x^c\]
c is a constant \[f^,\left(x\right)\,=\,cx^{c-1}\]
The derivative of a sum of two functions f, g and constants a, b:
\[\left(af+bg\right)^,\,=\, af^,+ bg^,\]The product rule for two functions f, g gives:
\[\left(fg\right)^,\,=\,f^,g+fg^,\]The quotient rule for functions f, g, where g ≠ 0, states that:
\[\left(\frac{f}{g}\right)^,\,=\,\frac{f^,g-fg^,}{g^2}\]
