Garden party with an electric kettle
Task number: 283
The electric kettle in the garden is connected to a 230-V line in the house via a 60 m long cable with a resistance 1.2 Ω. There is the following label on the kettle:
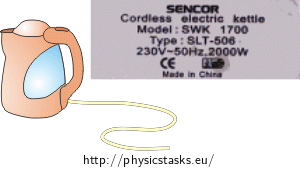
a) Find the actual voltage across the heating coil of the kettle and its actual input in this connection.
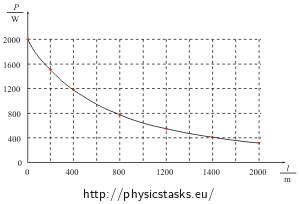
b) For this kettle and a given cross-section of the cable graph the input versus the length of the cable from 0 to 2 000 m.
Comment
We use the root mean square values of voltage and current hence we can handle the task as if the kettle is connected to a direct current circuit.
The root mean square values of voltage and current correspond to values of voltage and current at which the power of direct current in a circuit with resistance is the same as the power of alternating current.
Hint
The data on the label of the kettle give the value of the input at a given voltage and a given frequency. These values are characteristic for this kettle.
We use the root mean square values and consider only the resistance of the kettle thus we do not need the frequency of alternating current for our calculations.
Analysis
a) The actual voltage across the heating coil of the kettle and its actual input
Input of electric current is given as a product of the voltage across the appliance and the current through it. This current is equal to a quotient of the voltage across the appliance and its resistance. The values given on the label determine the parameters of the kettle hence it is possible to calculate the resistance of the kettle from the voltage and input written on it.
We can consider the cable and the kettle as two resistors connected in series therefore the current through them is equal. To find this current we insert the voltage across the source (i.e. 230-V line in the house) and the total resistance of the circuit into the Ohm’s law. The actual voltage across the kettle is directly proportional to the current through it and to its resistance.
Now we know the current through and the voltage across the kettle so we can find its actual input.
b) The dependence of the input to the kettle on the length of the cable
The resistance of a metal conductor is directly proportional to its length and inversely proportional to its cross-section. Furthermore, it depends on the resistivity of the conductor (i.e. the material of the conductor).
The cross-section and resistivity remain the same if the length of the cable is changed. We know the resistance of the cable of a given length thus we can use these two variables to express the unknown quotient of resistivity and cross-section. This quotient we insert into the expression of the resistance of the cable as a function of its length.
To find the dependence of input to the kettle on the length of the cable we use the expression for input that we derived in a) and substitute the resistance of the cable from the equation expressing the resistance of a cable as a function of its length.
Solution of the part a): The actual voltage across the heating coil of the kettle
We can consider the cable and the kettle as two resistors connected in series. R0 denotes the resistance of the cable, R denotes the resistance of the electric kettle (the heating coil).
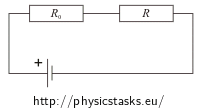
We know from the Ohm’s law that the current I through the circuit is given by:
\[I\,=\,\frac{U_0}{R_0+R}\]where I0 stands for the voltage across the source.
We consider the cable and the kettle as two resistors connected in series hence the total current through the circuit is equal to the current through the appliance:
\[I\,=\,\frac{U}{R}\]Comparing these two equations:
\[\frac{U_0}{R_0+R}\,=\,\frac{U}{R}\]we can express the actual voltage across the heating coil:
\[U\,=\,\frac{U_0R}{R_0+R}\tag{*}\]The label on the electric kettle reads 230 V and 2 000 W. That tells us that if we connect the kettle to the source with the voltage Us = 230 V its input is going to be Ps = 2 000 W. From these values we calculate the resistance of the kettle R.
The input to the kettle is given by:
\[P_s\,=\,U_sI\,=\,\frac{U_s^2}{R}\]where Us stands for the voltage across the kettle and R is the resistance of the kettle.
We express the resistance R from this equation and insert the values from the label. We obtain the resistance of the heating coil:
\[R\,=\,\frac{U_s^2}{P_s}\]We insert the resistance of the heating coil into the equation (*):
\[U\,=\,\frac{U_0\frac{U_s^2}{P_s}}{R_0+\frac{U_s^2}{P_s}}\,=\,\frac{U_0U_s^2}{P_s\left(R_0+\frac{U_s^2}{P_s}\right)}\]and we obtain the actual voltage across the heating coil of the electric kettle:
\[U\,=\,\frac{U_0U_s^2}{P_sR_0+U_s^2}\]Now we can insert the given numerical values: U0 = 230 V, R0 = 1.2 Ω, Ps = 2 000 W, Us = 230 V
\[U\,=\,\frac{230^3}{2\,000{\cdot}1.2+230^2}\,\mathrm{V}\,=\,220\,\mathrm{V}\]Solution of the part a): The actual input to the kettle
We calculate the actual input to the kettle from the expression:
\[P\,=\,\frac{U^2}{R}\]where R stands for the resistance of the heating coil and U stands for the actual voltage across the heating coil. These quantities have been determined in the previous section:
\[R\,=\,\frac{U_s^2}{P_s}\] \[U\,=\,\frac{U_0U_s^2}{P_sR_0+U_s^2}\]We insert both expressions into the equation for the actual input to the heating coil:
\[P\,=\,\frac{U_0^2U_s^4}{\left(P_sR_0+U_s^2\right)^2}\,\,\frac{P_s}{U_s^2}\]Thus for the actual input to the heating coil it holds:
\[P\,=\,\frac{U_0^2U_s^2P_s}{\left(P_sR_0+U_s^2\right)^2}\]Now we can calculate the numerical value of the actual input P:
U0 = 230 V, Ps = 2 000 W, Us = 230 V, R0 = 1.2 Ω
\[P\,=\,\frac{230^4{\cdot}2\,000}{\left(2\,000{\cdot}1.2+230^2\right)^2}\,\mathrm{W}\,=\,1\,830\,\mathrm{W}\]Solution of the part b): The dependence of the electrical input on the length of the cable
We derive the expression for the actual input to the electric kettle in the previous section:
\[P\,=\,\frac{U_0^2U_s^2P_s}{\left(P_sR_0+U_s^2\right)^2}\tag{**}\]The resistance of the wire changes with its length – the resistance of the metal wire is directly proportional to its length:
\[R\,=\,\rho\frac{l}{S}\]where ρ denotes the resistivity of the cable (depends on the material), l denotes the length and S denotes the cross-section of the cable.
The resistivity and the cross-section remain constant hence for the resistance of the cable of the length l0 it holds:
\[R_0\,=\,\rho\frac{l_0}{S}\hspace{10px}\Rightarrow\hspace{10px}\frac{\rho}{S}\,=\,\frac{R_0}{l_0}\]Therefore, we can calculate the resistance of metallic conductor from the equation:
\[R\,=\,\frac{l}{l_0}R_0\]If we want to examine the dependence of the input to the kettle on the length of the cable we have to replace the resistance R0 in the expression (**) by the resistance R which depends on the length of the cable:
\[P\,=\,\frac{U_0^2U_s^2P_s}{\left(RP_s+U_s^2\right)^2}\,=\,\frac{U_0^2U_s^2P_s}{\left(\frac{R_0}{l_0}lP_s+U_s^2\right)^2}\]We can further simplify this relation:
\[P\,=\,\frac{U_0^2U_s^2P_s}{\left(\frac{lR_0P_s+U_s^2l_0}{l_0}\right)^2}\]and obtain the input of the kettle as a function of the length of the cable. This function is given by the expression:
\[P\,=\,\frac{U_0^2U_s^2P_sl_0^2}{\left(U_s^2l_0+R_0P_s\bf{l}\right)^2}\]It is a rational function with a quadratic polynomial in l in the denominator. The length of the cable l is emphasized in the last equation.
The known numerical values are:
U0 = 230 V, Ps = 2 000 W, Us = 230 V, l0 = 60 m, R0 = 1.2 Ω
Now we can set the table for l from 0 to 2 000 m and graph the dependence of the input to the kettle on the length of the cable:
Here you can find the data file made in Excel.l [m] 0 400 800 1 200 1 600 2 000 P [W] 2 000 1 179 776 550 410 317 Answer of the part a)
The actual voltage across the heating coil of the kettle is 220 V and its actual input is 1 830 W.