Collection of Solved Problems in Physics

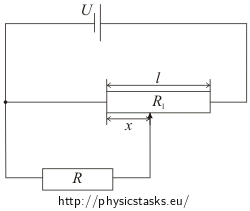
Potentiometer

Task number: 284

A potentiometer made from homogenous resistance wire of length l and resistance R_l = al is used to changed voltage at an appliance of resistance R.

Find the voltage across and current through a resistor R as a function of the distance x of the sliding contact from the end of the potentiometer.

• Hint

  Try to draw the circuit with the potentiometer divided into two parts.

• Analysis

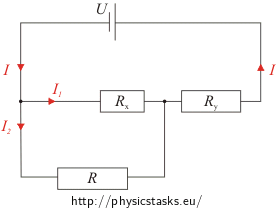
  Let us redraw the circuit with the potentiometer divided by the sliding contact into two parts with resistances R_x and R_y (see Illustrating picture). We can find the resistances of each part directly. The resistance of a conductor is a linear function of its length thus the resistance of the part of the potentiometer is directly proportional to the length of the resistance wire used in this part of the potentiometer.

  Let us label all the currents through different loops of the circuit in the picture.

  We need to find the current I₂ through the resistor R therefore we express all currents as functions of I₂. The current I is a sum of currents I₁ and I₂. The resistors R and R_x are in parallel connection thus there must be equal drop of voltage across them. That helps to express the current I₁ as a function of I₂.

  We know the total voltage across the circuit hence we can express the emf (electromotive force) as a sum of drops of voltage across resistors R_x and R_y.

  From the expression for the total voltage we obtain the current I₂.

  The voltage across the resistor R is given as a product of the resistance of the resistor and the current through this resistor.

• Illustrating picture

  Let us redraw the circuit with the potentiometer divided by the sliding contact into two parts with resistances R_x and R_y and label all the currents through different loops of the circuit.

  

• Solution

  The expression for the resistance of the potentiometer reads

  \[R_x+R_y\,=\,R_l\,=\,al\]

  where l stands for the length of the whole potentiometer and a is a constant of proportionality.

  The resistance of a wire is a linear function of its length thus we can express the resistances of the resistors R_x and R_y express as:

  \[R_x\,=\,ax\] \[R_y\,=\,a\left(l-x\right)\]

  Our goal is to find the current I₂ through the resistor R thus we express all currents as functions of I₂.

  The algebraic sum of the currents into any junction is zero.

  \[I\,=\,I_1+I_2\]

  The resistor with the resistance R and the part of the potentiometer with resistance R_x are in parallel connection thus:

  \[RI_2\,=\,R_xI_1\,=\,axI_1\]

  We express the current I₁ as

  \[I_1\,=\,\frac{R}{ax}I_2\tag{*}\]

  Since the total voltage across the circuit is known we can express the emf (electromotive force) as a sum of drops of voltage across resistors. Hence:

  \[U\,=\,R_xI_1+R_yI\,=\,axI_1+a\left(l-x\right)\left(I_1+I_2\right)\] \[U\,=\,alI_1+a\left(l-x\right)I_2\]

  Inserting the expression (*) into this equation we obtain:

  \[U\,=\,al\frac{R}{ax}I_2+a\left(l-x\right)I_2\] \[U\,=\,\left(\frac{l}{x}R+a\left(l-x\right)\right)I_2\]

  We determine the constant of proportionality from the expression:

  \[R_l\,=\,al\hspace{10px}\Rightarrow\hspace{10px}a\,=\,\frac{R_l}{l}\]

  and insert it into the equation for the total voltage:

  \[U\,=\,\left(\frac{l}{x}R+\frac{R_l}{l}\left(l-x\right)\right)I_2\]

  Now we can express the current I₂ through the resistor R:

  \[I_2\,=\,\frac{U}{\frac{l}{x}R+\frac{R_l}{l}\left(l-x\right)}\]

  and simplifying we obtain:

  \[I_2\,=\,\frac{U}{\frac{l^2R+R_lx\left(l-x\right)}{xl}}\]

  The final expression for the current through the resistor as a function of the distance x of the sliding contact from the end of the potentiometer reads:

  \[I_R\,=\,\frac{xlU}{l^2R+R_lx\left(l-x\right)}\]

  The voltage across the resistor is given as a product of the current through this resistor and the resistance of the resistor:

  \[U_R\,=\,I_RR\] \[U_R\,=\,\frac{xlUR}{l^2R+R_lx\left(l-x\right)}\]

• Answer

  The voltage across and current through the resistor R as functions of the distance x of the sliding contact from the end of the potentiometer are given by the expressions:

  \[I_R\,=\,\frac{xlU}{l^2R+R_lx\left(l-x\right)}\] \[U_R\,=\,\frac{xlUR}{l^2R+R_lx\left(l-x\right)}\]