Charged Balls Hanging on a String
Task number: 1551
Two small balls with a mass of 0.5 g are hanging on two separate strings 1 m long attached to a common point. They are given an identical charge and spread apart to a distance 4 cm from each other.
Determine the charge of the balls.
Hint
What are the forces acting on the balls and what is their direction? Draw a picture.Analysis
Two forces act on each ball hanging on the string: a force of gravity and tension of the string. The balls are also charged, so they repel one another with electric force. We determine its size using Coulomb's law.
Both balls are at rest, so the net force must be zero. To satisfy this postulate, the vector sum of electric force and the force of gravity must be of the same size and opposite direction as the tension of the string. In the picture we can find two similar triangles ("green" and "purple"). From the similarities of the two triangles we can express the unknown size of electric force and thus the charge of the balls.
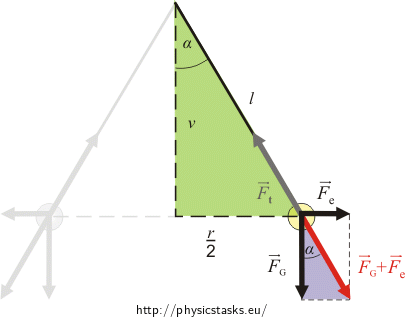
Figure of forces acting on the balls
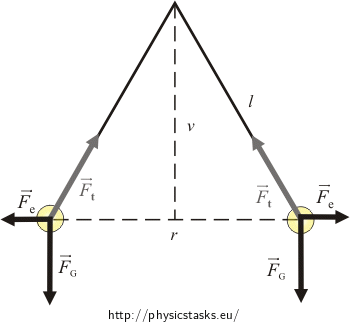
Solution
Two forces act on each ball hanging on the string: the force of gravity \( \vec{F}_G\) and tension of the string \( \vec{F}_t\). . In addition, the balls are charged with an identical charge, therefore there is one more force: a repulsive electric force \( \vec{F}_e\).
The size of the repulsive electric forces is determined from Coulomb's law:
\[F_e \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q_1 Q_2}{r^2}\,.\]Both balls are charged with identical charge Q; thus we can simplify the equation:
\[F_e \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q^2}{r^2}\,.\]Since the balls are at rest, the net force acting on the balls is equal to zero.
The force \(\vec{F}_e+\vec{F}_G\)must act in the opposite direction than the tension of the string \(\vec{F}_t\). Thanks to this, the "green" and "purple" triangles are similar. From the "purple" triangle we can express tg α.
\[\mathrm{tg}\,\alpha\,=\,\frac{F_e}{F_G}\,=\,\frac{\frac{1}{4\pi\varepsilon_0}\,\frac{Q^2}{r^2}}{mg}\,=\,\frac{Q^2}{4 \pi\varepsilon_0mgr^2}\]The angle α is also found in the similar "green" triangle. Again, we express the tangent of this angle.
\[\mathrm{tg}\,\alpha\,=\,\frac{\frac{r}{2}}{v}\,=\,\frac{r}{2v}\]The side v of the "green" triangle is determined using the Pythagorean Theorem \(v\,=\,\sqrt{ l^2-(\frac{r}{2})^2}.\) After substitution
\[\mathrm{tg}\,\alpha\,=\,\frac{r}{2 \sqrt{ l^2-(\frac{r}{2})^2} }\,=\,\frac{r}{ \sqrt{ 4l^2-r^2} }.\]Now there are two equations for the tangent of the angle α. We compare them
\[\frac{Q^2}{4 \pi \varepsilon_0 mgr^2}\,=\,\frac{r}{\sqrt{ 4l^2-r^2} } \]and evaluate the unknown charge Q:
\[Q^2\,=\,\frac{4 \pi \varepsilon_0 mgr^3}{\sqrt{ 4l^2-r^2} } ,\] \[Q\,=\,\sqrt{\frac{4 \pi \varepsilon_0 mgr^3}{\sqrt{ 4l^2-r^2} } }.\]Given values and numerical insertion:
\(m\,=\,0.5\,\mathrm{g}\,=\,5{\cdot} 10^{-4}\,\mathrm{kg}\) Mass of the balls \(l\,=\,1\,\mathrm{m}\) Length of the string \(r\,=\,4\,\mathrm{cm}\,=\,4{\cdot} 10^{-2}\,\mathrm{m}\) Distance of the balls \(Q\,=\,?\,\left(\mathrm{C}\right)\) Constants from The Handbook of Chemistry and Physics:
\(\varepsilon_0\,=\,8.85{\cdot} 10^{-12}\,\mathrm{ C^2\,N^{-1}\,m^{-2}}\) \(g\,=\,9.8\,\mathrm{ m\,s^{-2}}\)
\[\begin{eqnarray} Q\,&=&\,\sqrt{\frac{4 \pi \varepsilon_0 mgr^3}{\sqrt{ 4l^2-r^2} } }\\ Q\,&=&\,\sqrt{\frac{4\pi \,\cdot\,8.85{\cdot} 10^{-12}\, \cdot \,5{\cdot} 10^{-4}\, \cdot\,9.8 \,\cdot\, \left(4 {\cdot}10^{-2}\right)^3}{ \sqrt{ 4 {\cdot} 1^2-\left(4 {\cdot}10^{-2}\right)^2}}}\,\mathrm{C}\\ Q\,&\dot=&\,4.2{\cdot}10^{-9}\,\mathrm{C}\,\dot=\,4.2\,\mathrm{nC} \end{eqnarray}\]Answer
Each ball was charged with a charge \(Q\,=\,\sqrt{\frac{4 \pi \varepsilon_0 mgr^3}{\sqrt{ 4l^2-r^2} }} \,\dot=\,4.2\,\mathrm{nC} \).
Link to a more difficult task
In the task Two balls on a thread immersed in benzene the balls are immersed in benzene.




