Praca, ciepło i zmiana energii wewnętrznej tlenu
Kod zadania: 1057
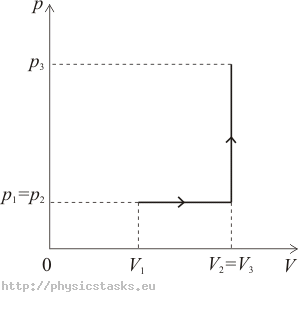
Początkowa objętość tlenu wynosi 5 l, a jego ciśnienie 100 kPa. Najpierw poddajemy go izobarycznemu ogrzewaniu do dwukrotnej objętości, a następnie izochorycznie zwiększamy jego ciśnienie do wartości czterokrotnie większej niż ciśnienie początkowe. Określ, jaką pracę wykonał gaz, jaką wartość ciepła mu dostarczyliśmy i jak się zmieniła jego energia wewnętrzna.
Zapis danych
V1 = 5 l = 0,005 m3 początkowa objętość tlenu p1 = 100 kPa = 105 Pa początkowe ciśnienie tlenu V2 = 2V1 objętość po ogrzaniu p3 = 4p1 izochoryczny wzrost ciśnienia W = ? praca wykonana Q = ? dostarczone ciepło ΔU = ? zmiana energii wewnętrznej Diagram p–V
Podpowiedź 1 – określenie ciepła
Do obliczenia ciepła dostarczonego w przemianie izobarycznej skorzystamy ze związku pomiędzy ciepłem Q a ciepłem molowym Cp przy stałym ciśnieniu
\[Q=nC_p\mathrm{\Delta}T,\]gdzie n to liczba moli, a ΔT zmiana temperatury gazu.
Do obliczenia ciepła dostarczonego w przemianie izochorycznej skorzystamy z podobnego związku między ciepłem Q a ciepłem molowym CV przy stałej objętości
\[Q=nC_V\mathrm{\Delta}T,\]gdzie n to liczba moli, a ΔT zmiana temperatury gazu.
Podpowiedź 2 – ciepło molowe tlenu
Ciepło molowe tlenu przy stałym ciśnieniu wynosi
\[C_p=\frac{7}{2}R.\]Ciepło molowe tlenu przy stałej objętości wynosi
\[C_V=\frac{5}{2}R.\]Podpowiedź 3 – określenie zmiany temperatury
Aby określić zmianę temperatury w przemianie izobarycznej, skorzystamy z prawa Gay-Lussaca, zaś w przemianie izochorycznej - z prawa Charlesa.
Rozwiązanie – ciepło dostarczone
Całkowite ciepło dostarczone jest sumą ciepła dostarczonego w przemianie izobarycznej i ciepła dostarczonego w przemianie izochorycznej.
Ciepło dostarczone w przemianie izobarycznej obliczymy jako iloczyn liczby moli, ciepła molowego przy stałym ciśnieniu i zmiany temperatury w przemianie. Zmianę temperatury określimy z prawa Gay-Lussaca. Skorzystamy też z równiania stanu gazu doskonałego, aby obliczyć ciepło przy pomocy zadanych wielkości.
Analogicznie postąpimy przy określaniu ciepła dostarczonego w przemianie izochorycznej. W tym przypadku korzystać będziemy z ciepła molowego przy stałej objętości oraz prawa Charlesa.
Obliczenie ciepła dostarczonego
Ponieważ dodawać będziemy ciepło dostarczane gazowi w dwóch procesach, na całkowite ciepło Q możemy zapisać wzór
\[Q=Q_1+Q_2,\]gdzie Q1 i Q2 to odpowiednio ciepła dostarczone w przemianach izobarycznej i izochorycznej.
Do obliczenia ciepła Q1 dostarczonego w przemianie izobarycznej skorzystamy ze związku pomiędzy ciepłem a ciepłem molowym Cp przy stałym ciśnieniu
\[Q_1=nC_p\left(T_2-T_1\right),\]gdzie n jest liczbą moli, T2 i T1 to temperatury końcowa i początkowa gazu.
Ponieważ tlen jest gazem dwuatomowym, jego ciepło molowe przy stałym ciśnieniu
\[C_p=\frac{7}{2}R\]możemy więc zapisać
\[Q_1=\frac{7}{2}nR\left(T_2-T_1\right).\]Zgodnie z prawem Gay-Lussaca, jeśli dwukrotnie wzrośnie objętość, to również dwukrotnie wzrośnie temperatura, czyli T2 = 2T1. Po podstawieniu do poprzedniego wyrażenia otrzymamy
\[Q_1=\frac{7}{2}nR\left(2T_1-T_1\right)=\frac{7}{2}nRT_1.\]Skorzystamy też z równania stanu gazu doskonałego
\[p_1V_1=nRT_1 \qquad\Rightarrow\qquad nT_1=\frac{p_1V_1}{R}.\]Po podstawieniu mamy
\[Q_1=\frac{7}{2}R\frac{p_1V_1}{R}=\frac{7}{2}p_1V_1.\]Na ciepło Q2 dostarczone w przemianie izochorycznej zapiszemy wzór
\[Q_2=nC_V\left(T_3-T_2\right).\]Ciepło molowe przy stałej objętości dla tlenu wynosi
\[C_V=\frac{5}{2}R\]a więc możemy zapisać
\[Q_2=\frac{5}{2}nR\left(T_3-T_2\right).\]Zgodnie z prawem Charlesa, jeśli ciśnienie wzrośnie czterokrotnie, to i temperatura rośnie cztery razy, czyli T3 = 4T2 = 8T1.
Po podstawieniu do poprzedniego wyrażenia
\[Q_2=\frac{5}{2}nR\left(8T_1-2T_1\right)=15nRT_1\]a z równania stanu gazu doskonałego
\[nT_1=\frac{p_1V_1}{R}\]otrzymamy więc na ciepło Q2 wzór
\[Q_2=15R\frac{p_1V_1}{R}=15p_1V_1.\]Całkowite ciepło dostarczone Q wynosi
\[Q=Q_1+Q_2=\frac{7}{2}p_1V_1+15p_1V_1,\] \[Q=\frac{37}{2}p_1V_1.\]Podpowiedź 4 – określenie pracy
Praca wykonana przez gaz w przemianie izobarycznej
\[W=p\left(V_2-V_1\right),\]gdzie p jest ciśnieniem gazu, V1 i V2 to objętości gazu przed i po przemianie.
W przemianie izochorycznej objętość gazu jest stała, praca nie jest wykonywana.
Podpowiedź 5 – zmiana energii wewnętrznej
Do określenia zmiany energii wewnętrznej ΔU wykorzystaj 1. zasadę termodynamiki.
Rozwiązanie – praca wykonana i zmiana energii wewnętrznej
Przede wszystkim zauważmy, że gaz wykonuje pracę tylko w przemianie izobarycznej. Tę pracę obliczamy jako iloczyn ciśnienia i zmiany objętości gazu w przemianie.
Zmianę energii wewnętrznej określamy z 1. zasady termodynamiki.
Obliczenie pracy wykonanej i zmiany energii wewnętrznej
Praca W wykonana przez gaz w przemianie izobarycznej
\[W=p_1\left(V_2-V_1\right),\]gdzie p1 to ciśnienie gazu, V1 i V2 to objętość gazu przed i po przemianie.
Po podstawieniu za objętość V2
\[W=p_1\left(2V_1-V_1\right)\]otrzymamy
\[W=p_1V_1.\]Zmianę energii wewnętrznej ΔU określamy z 1. zasady termodynamiki jako różnicę dostarczonego ciepła Q i pracy wykonanej W
\[\Delta U=Q-W=\frac{37}{2}p_1V_1 -p_1V_1= \frac{35}{2}p_1V_1.\]Rozwiązanie liczbowe
\[Q=\frac{37}{2}p_1V_1=\frac{37}{2}\cdot0{,}005\cdot{10^5}\,\mathrm{J} = 9250 \,\mathrm{J} = 9{,}25\,\mathrm{kJ}\] \[W=p_1V_1=0{,}005\cdot{10^5}\,\mathrm{J}=500\,\mathrm{J}\] \[\Delta U=Q-W=\left(9250-500\right)\,\mathrm{J}=8750\,\mathrm{J}=8{,}75\,\mathrm{kJ}\]Odpowiedź
Gaz wykonał pracę 500 J, dostarczono mu 9,25 kJ ciepła, a przyrost jego energii wewnętrznej wynosi 8,75 kJ.



