Spadający swobodnie kamień
Kod zadania: 1097
Spadający swobodnie kamień ma w pewnym położeniu prędkość chwilową 5 m·s−1, a w innym, niżej położonym miejscu, prędkość ta wynosi 8 m·s−1. W ciągu jakiego czasu kamień pokona drogę od jednego położenia do drugiego i jaka jest odległość tych punktów?
Zapis danych
v1 = 5 m·s−1 prędkość kamienia w pierwszym położeniu v2 = 8 m·s−1 prędkość kamienia w niższym położeniu t = ? (s) czas, w którym kamień pokona odcinek od pierwszego położenia do drugiego s = ? (m) odległość obu punktów na drodze Z tablic: g = 9,81 m·s−2 przyspieszenie grawitacyjne Podpowiedź 1: Czas przelotu z pierwszego położenia do drugiego
Jakim ruchem porusza się kamień? Przypomnij sobie zależność szybkości od czasu w tym ruchu.
Jak obliczysz czas przelotu kamienia z jednego położenia do drugiego? Czy znasz wszystkie wielkości potrzebne do obliczeń?
Podpowiedź 2 : Odległość obu położeń
Wiemy, że kamień spada swobodnie. Jak można określić odległość dwóch położeń, czyli drogę, którą pokonał pomiędzy pierwszym a drugim położeniem?
Do obliczeń wykorzystaj wzory (1), (2) z rozwiązania poprzedniej podpowiedzi.
PEŁNE ROZWIĄZANIE
Czas przelotu z położenia 1 do położenia 2
Kamień porusza się ruchem jednostajnie przyspieszonym.
Zależność prędkości od czasu w takim przypadku określa wzór: \(v(t) \,=\, gt\)
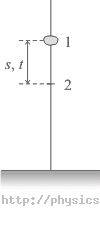
Przedział czasu t, w którym kamień przemieści się z jednego położenia do drugiego, określimy jako różnicę czasów, w których kamień był w położeniach 2 i 1 (patrz rysunek), czyli:
\[t\,=\,t_2\,-\,t_1\]Z treści zadania wiemy, że chodzi o spadek swobodny. Prędkość w położeniu 1 wynosi:
\[v_1 \,=\, gt_1\,.\]Stąd:
\[t_1 \,=\, \frac{v_1}{g}\,.\tag{1}\]Prędkość w położeniu 2 wynosi:
\[v_2 \,=\, gt_2\,.\]Stąd:
\[t_2 \,=\, \frac{v_2}{g}\,.\tag{2}\]Na czas t otrzymujemy:
\[t\,=\,\frac{v_2}{g}\,-\,\frac{v_1}{g}\,=\,\frac{v_2\,-\,v_1}{g}\,.\]Po podstawieniu danych liczbowych:
\[t\,=\,\frac{8\,-\,5}{9{,}81}\,\mathrm{s}\,\dot=\,0{,}3\,\mathrm{s}\,.\]Odległość położeń 1 i 2
Zależność drogi od czasu przy spadaniu swobodnym (ruch jednostajnie przyspieszony) opisuje zależność:
\[s \,=\, \frac{1}{2}\,gt^{2}\,.\]Odległość położeń 1 i 2 określimy jako różnicę drogi, którą kamień pokonał do położenia 2 i drogi, którą pokonał do położenia 1.
\[s\,=\,s_2\,-\,s_1\,=\,\frac{gt_2^{2}}{2}\,-\,\frac{gt_1^{2}}{2}\,=\,\frac{g}{2}\,\left(t_2^{2}\,-\,t_1^{2}\right)\]Za t2 i t1 podstawimy ze wzorów (1) i (2):
\[s\,=\,\frac{g}{2}\,\left(\frac{v_2^{2}}{g^{2}}\,-\,\frac{v_1^{2}}{g^{2}}\right)\,=\,\frac{1}{2g}(v_2^{2}\,-\,v_1^{2})\]Po podstawieniu danych liczbowych:
\[s\,=\,\frac{1}{2{\cdot} 9{,}81}\cdot(8^{2}-5^{2})\,\mathrm{m}\,\dot=\,2\,\mathrm{m}\,.\]Odpowiedź
Kamień dotrze z pierwszego do drugiego położenia w czasie
\[t\,=\,\frac{v_2\,-\,v_1}{g}\,\dot=\,0{,}3\,\mathrm{s}\,.\]Odległość tych dwóch położeń wynosi
\[s\,=\,\frac{1}{2g}(v_2^{2}\,-\,v_1^{2})\,\dot=\,2\,\mathrm{m}\,.\]



