Zbiór rozwiązanych zadań i problemów fizycznych

Kamyk na skalnej półce

Kod zadania: 1098

• Podpowiedź 1: Oznaczenia

  Wprowadźmy oznaczenia na odcinki, na które podzielimy wysokość h, oraz na czasy spadania w poszczególnych częściach (jednakowe).

• Rozwiązanie podpowiedzi 1

  Odcinki spadania kamyka oznaczymy jako:  \(x_1, x_2,..., x_n \,.\)

  Czas spadania, jednakowy dla wszystkich części, oznaczymy  t₀.

   

   

  

   

• Podpowiedź 2 : Droga spadania

  Poszczególne odcinki składają się na całkowitą drogę, którą pokonuje kamyk spadając swobodnie ze skalnej półki.

  Jaki jest związek między drogą w spadku swobodnym a czasem spadku? Zapisz odpowiednie równanie dla pierwszego odcinka, następnie dla dwóch pierwszych odcinków, a potem dla n odcinków.

• Rozwiązanie podpowiedzi 2

  Poszczególne części możemy traktować jako odcinki drogi, którą pokonuje kamyk spadając swobodnie ze skalnej półki.

   

  Zapiszmy sumę poszczególnych odcinków: \(h=x_1+x_2+...+x_n\).

  Czas spadania, taki sam dla kolejnych części, oznaczyliśmy t₀.

  Mamy więc:

  \[x_1=\frac{gt_0^{2}}{2}\,,\tag{1}\] \[x_1+x_2=\frac{g(2t_0)^{2}}{2}\,,\tag{2}\] \[h=x_1+x_2+...+x_n=\frac{g(nt_0)^{2}}{2}\,.\tag{3}\]

• Podpowiedź 3: Czas spadania

  Ze wzoru (3) z rozwiązania poprzedniej podpowiedzi można łatwo określić czas spadania t₀ dla poszczególnych odcinków (jednakowy).

• Rozwiązanie podpowiedzi 3

  Czas spadania t₀ dla poszczególnych odcinków wyznaczony z równania (3) wynosi:

  \[t_0^{2}=\frac{2h}{g}\frac{1}{n^{2}}\,.\tag{4}\]

• Podpowiedź 4: Rozdzielenie drogi spadania na części

  Wykorzystaj wzór (4) na czas spadania z rozwiązania poprzedniej podpowiedzi i określ jednakowe odcinki drogi x_i na podstawie wysokości spadania h dla n części.

• Rozwiązanie podpowiedzi 4

  Na czas t₀ mamy:

  \[t_0^{2}=\frac{2h}{g}\frac{1}{n^{2}}\,.\tag{4}\]

   

  Podstawmy wyrażenie na t₀ do wzoru (1) dla 1. odcinka drogi:

  \[x_1=\frac{gt_0^{2}}{2}=\frac{h}{n^{2}}\,.\]

  Drugi odcinek określimy ze wzoru (2), ponownie podstawiając za t₀:

  \[x_2=\frac{g(2t_0)^{2}}{2}-x_1=h\left(\frac{2}{n}\right)^{2}-h\left(\frac{1}{n}\right)^{2}=\frac{3h}{n^{2}}\,.\]

  Dla i-tego odcinka otrzymamy:

  \[x_i=\frac{1}{2}g(it_0)^{2}-\frac{1}{2}g[(i-1)t_0]^{2}=\frac{gt_0^{2}}{2}(2i-1)=\frac{g}{2}.\frac{2h}{g}.\frac{1}{n^{2}}(2i-1)\,,\] \[x_i=\frac{2i-1}{n^{2}}h\,.\]

  Podstawiając dane liczbowe:

  dla: \(i=1{,}2,...,5\),\(h=245\,\mathrm{m} \), \(n=5\) otrzymamy:

   

  \[x_1=\frac{245}{25}\,\mathrm{m}=9{,}8\,\mathrm{m}\,,\] \[x_2=\frac{3.245}{25}\,\mathrm{m}=29{,}4\,\mathrm{m}\,,\] \[x_3=\frac{5.245}{25}\,\mathrm{m}=49{,}0\,\mathrm{m}\,,\] \[x_4=\frac{7.245}{25}\,\mathrm{m}=68{,}6\,\mathrm{m}\,,\] \[x_5=\frac{9.245}{25}\,\mathrm{m}=88{,}2\,\mathrm{m}\,.\]

   

• PEŁNE ROZWIĄZANIE

  Poszczególne odcinki spadku kamyka oznaczymy:  \(x_1, x_2,..., x_n \,.\)

  Czas spadania, jednakowy dla każdego odcinka, oznaczmy t₀.

   

   

  

   

   

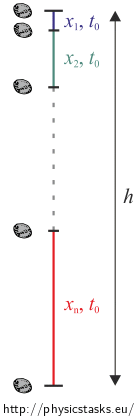
  Poszczególne odcinki to fragmenty drogi, którą kamyk pokonuje spadając swobodnie ze skalnej półki.

   

  Ich sumę zapiszemy jako: \(h=x_1+x_2+...+x_n\).

  Zachodzi też:

  \[x_1=\frac{gt_0^{2}}{2}\,,\tag{1}\] \[x_1+x_2=\frac{g(2t_0)^{2}}{2}\,,\tag{2}\] \[h=x_1+x_2+...+x_n=\frac{g(nt_0)^{2}}{2}\,.\tag{3}\]

  Czas spadania t₀ dla poszczególnych odcinków obliczamy ze wzoru (3):

  \[t_0^{2}=\frac{2h}{g}\frac{1}{n^{2}}\,.\tag{4}\]

   

  Podstawmy wyrażenie na t₀ do wzoru (1) dla 1. odcinka:

  \[x_1=\frac{gt_0^{2}}{2}=\frac{h}{n^{2}}\,.\]

  Drugi odcinek określimy ze wzoru (2), ponownie podstawiając za t₀:

  \[x_2=\frac{g(2t_0)^{2}}{2}-x_1=h\left(\frac{2}{n}\right)^{2}-h\left(\frac{1}{n}\right)^{2}=\frac{3h}{n^{2}}\,.\]

  Dla i-tego odcinka zapiszemy:

  \[x_i=\frac{1}{2}g(it_0)^{2}-\frac{1}{2}g[(i-1)t_0]^{2}=\frac{gt_0^{2}}{2}(2i-1)=\frac{g}{2}.\frac{2h}{g}.\frac{1}{n^{2}}(2i-1)\,,\] \[x_i=\frac{2i-1}{n^{2}}h\,.\]

  Podstawiając dane liczbowe:

  dla: \(i=1{,}2,...,5\),\(h=245\,\mathrm{m} \), \(n=5\) otrzymamy:

   

  \[x_1=\frac{245}{25}\,\mathrm{m}=9{,}8\,\mathrm{m}\,,\] \[x_2=\frac{3.245}{25}\,\mathrm{m}=29{,}4\,\mathrm{m}\,,\] \[x_3=\frac{5.245}{25}\,\mathrm{m}=49{,}0\,\mathrm{m}\,,\] \[x_4=\frac{7.245}{25}\,\mathrm{m}=68{,}6\,\mathrm{m}\,,\] \[x_5=\frac{9.245}{25}\,\mathrm{m}=88{,}2\,\mathrm{m}\,.\]

   

• Odpowiedź

  Na poszczególne odcinki spadku kamyka ze skalnej półki otrzymujemy wyrażenia:

  \[x_1=\frac{h}{n^{2}}\,,\] \[x_2=\frac{3h}{n^{2}}\,,\] \[x_i=\frac{2i-1}{n^{2}}h\,.\]

   

  Dla \(i=1{,}2,...,5\); \(h=245\,\mathrm{m} \); \(n=5\) otrzymamy:

  \[x_1=9{,}8\,\mathrm{m}\,,\] \[x_2=29{,}4\,\mathrm{m}\,,\] \[x_3=49{,}0\,\mathrm{m}\,,\] \[x_4=68{,}6\,\mathrm{m}\,,\] \[x_5=88{,}2\,\mathrm{m}\,.\]