Dziewczynka ciągnie sanki po zaśnieżonym chodniku

Kod zadania: 883

Dziewczynka ciągnie sanki o masie 20 kg po płaskim zaśnieżonym chodniku. Szybkość sanek jest stała. Współczynnik tarcia dynamicznego między płozami a chodnikiem wynosi 0,1; kąt pomiędzy płozami a chodnikiem wynosi 30°. Wyznacz:

1) przyspieszenie sanek

2) wartość siły, którą dziewczynka działa na sanki

3) wartość siły nacisku, którą sanki działają na chodnik

4) wartość siły tarcia działającej na sanki

Zapis danych

m = 20 kg	masa sanek
f_d = 0,1	współczynnik tarcia dynamicznego między płozami a chodnikiem
φ = 30°	kąt pomiędzy płozami a chodnikiem
a = ? (m s^-2)	przyspieszenie sanek
T = ? (N)	wartość siły, którą dziewczynka działa na sanki
N = ? (N)	wartość siły nacisku sanek na chodnik
F_t = ? (N)	wartość siły tarcia działającej na sanki

Podpowiedź 1 - przyspieszenie sanek, siły działające na sanki
Zastanów się, co oznacza warunek stałej szybkości - jakie to ma konsekwencje, jeśli chodzi o przyspieszenie (a więc i siłę wypadkową). Naszkicuj ilustrację, zaznaczając na niej wszystkie siły działające na sanki. Wykorzystaj 2. zasadę dynamiki Newtona (\(\mathrm{\Sigma}\vec{F}\,=\,m\vec{a}\)) i napisz równanie ruchu dla sanek.
Rozwiązanie podpowiedzi 1 - przyspieszenie sanek, siły działające na sanki
Przyspieszenie sanek:

Ponieważ szybkość sanek jest stała, ich przyspieszenie wynosi zero (\(\vec{a}\,=\,0\)).

Siły działające na sanki:

\(\vec{F}_{G}\)…siła ciężkości

\(\vec{N}\)…siła reakcji, którą chodnik działa na sanki

\(\vec{T}\)…poszukiwana siła ciągu, z jaką dziewczynka ciągnie sanki

\(\vec{F}_{t}\)…siła tarcia pomiędzy sankami a chodnikiem

Równanie ruchu dla sanek:
\[ \vec{F}_{G}+ \vec{N} + \vec{T} + \vec{F}_{t} \,=\, m\vec{a} \,=\, 0 \tag{1}\]
Podpowiedź 2 - równanie ruchu skalarnie
Równanie ruchu powinniśmy zapisać skalarnie. Wprowadźmy układ współrzędnych, znajdźmy składowe sił w kierunkach osi układu i zapiszmy dla tych składowych równania ruchu.
Rozwiązanie podpowiedzi 2 - równanie ruchu skalarnie
Oś x przyjmiemy zgodnie z kierunkiem ruchu, a oś y prostopadle do podłoża.

Dla składowych wzdłuż osi x:
\[ T\cos\varphi - F_{t} \,=\, 0 \tag{2}\]
Dla składowych wzdłuż osi y:
\[N + T\sin\varphi - F_G \,=\, 0 \tag{3}\]
Uwaga: Zwykle przyjmujemy jedną z osi zgodnie z kierunkiem ruchu, a drugą prostopadle.
Podpowiedź 3 - wartość siły nacisku, siła ciągu
Zastanów się, od czego zależy wartość siły ciągu i jak możemy ją wyznaczyć.
Rozwiązanie podpowiedzi 3 - wartość siły nacisku, siła ciągu
Siłę tarcia wyznaczymy na podstawie siły nacisku sanek na chodnik, która zgodnie z 3. zasadą dynamiki Newtona jest równa sile reakcji chodnika na sanki.

Siłę tarcia F_t możemy więc zapisać jako:
\[F_t \,=\, Nf_d\tag{4}\]
Siłę N reakcji chodnika na sanki, otrzymamy z równania (3):
\[N \,=\, mg - T\sin{\varphi}\tag{5}\]
Z równań (4) i (5) uzyskamy:
\[F_{t} \,=\, f_{d}\left(mg - T\sin\varphi\right)\tag{6}\]
Wielkość (6) podstawiamy do równania (2):
\[T\cos\varphi - f_{d}(mg - T\sin\varphi) \,=\, 0\] \[T\cos\varphi - f_d mg + f_d T\sin\varphi \,=\, 0\] \[T(\cos\varphi + f_d\sin\varphi)-f_d mg\,=\, 0\tag{7}\]
Z równania (7) pozostaje już tylko wyrazić siłę ciągu:
\[T \,=\, \frac{mgf_{d}}{\cos\varphi + f_{d}\sin\varphi}\tag{8}\]
Podpowiedź 4 - wartość siły reakcji
Siła, którą sanki naciskają na chodnik, jest zgodnie z 3. zasadą dynamiki Newtona równa sile, którą chodnik działa na sanki. Wartość siły N, którą chodnik działa na sanki, została już określona w równaniu (5):
\[N \,=\, mg - T\sin{\varphi}\tag{5}\]
Trzeba jeszcze podstawić wyrażenie na siłę ciągu.
Rozwiązanie podpowiedzi 4 - wartość siły reakcji
Siła N, którą chodnik działa na sanki, jest określona równaniem (5):
\[N \,=\, mg - T\sin\varphi\tag{5}\]
Podstawimy za T wyrażenie (8), otrzymując:
\[N \,=\, mg - \frac{mgf_{d}}{\cos\varphi + f_{d}\sin\varphi}\sin\varphi \,=\, mg (1 - \frac{f_{d}\sin\varphi}{\cos\varphi + f_{d}\sin\varphi})\,=\] \[\,=\, mg(\frac{\cos\varphi}{\cos\varphi + f_{d}\sin{\varphi}}) \,=\, mg(\frac{1}{1 + f_{d}\tan\varphi})\tag{9}\]
Podpowiedź 5 - wartość siły tarcia
Wartość siły tarcia F_t została już określona wzorem (4):
\[F_{t} \,=\, Nf_{d}\tag{4}\]
Wystarczy podstawić wyrażenie na siłę nacisku.
Rozwiązanie podpowiedzi 5 - wartość siły tarcia
Siłę tarcia F_t określamy wzorem (4):
\[F_{t} \,=\, Nf_{d}\tag{4}\]
Podstawmy do równania (4) za N wyrażenie z równania (9), otrzymamy:
\[F_{t} \,=\, mg\left(\frac{1}{1 + f_{d}\tan\varphi}\right)f_{d}\tag{10}\]
Uwaga: Siła tarcia F_t nie jest juz określona jako mgf_d, gdyż ciągnięcie za sznurek przy sankach zmniejsza siłę nacisku na chodník, N jest więc mniejsze niż mg.
ROZWIĄZANIE LICZBOWE CZĘŚCI 1 - przyspieszenie sanek
Ponieważ prędkość sanek jest stała, nie zmienia się w czasie, zgodnie z definicją przyspieszenie sanek jest więc równe zeru (\(\vec{a} \,=\, 0\)).

Odpowiedź: Przyspieszenie sanek a wynosi zero.
ROZWIĄZANIE LICZBOWE CZĘŚCI 2 - wartość siły ciągu
Siły działające na sanki:

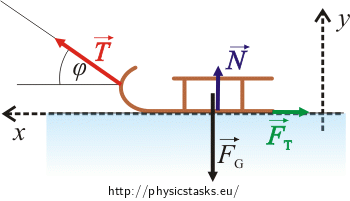
\(\vec{F}_{G} \)...siła ciężkości

\(\vec{N} \)...siła reakcji, którą chodnik działa na sanki

\(\vec{T}\)...poszukiwana siła ciągu, którą dziewczynka ciągnie sanki po chodniku

\(\vec{F}_{t}\)...sila tarcia sanek o chodnik

Równanie ruchu dla sanek:
\[\vec{F}_{G}+\vec{N}+\vec{T}+\vec{F}_{t}\,=\,m\vec{a}\,=\,0\tag{1}\]
m…masa sanek

\(\vec{a}\)…przyspieszenie sanek

Ponieważ prędkość \(\vec{v}\) jest stała, zgodnie z definicją przyspieszenie \(\vec{a}\) wynosi zero, a wypadkowa sił działających na sanki również wynosi zero.

Wprowadźmy układ współrzędnych i równanie ruchu (1) zapiszmy skalarnie. Kierunek osi x przyjmiemy zgodnie z kierunkiem ruchu, zaś osi y prostopadle - zgodnie z ilustracją.

Dla osi x:
\[ T\cos{\varphi} - F_{t} \,=\, 0 \tag{2}\]
Dla osi y:
\[N + T\sin{\varphi} - F_G \,=\, 0 \tag{3}\]
Siłę tarcia obliczymy na podstawie siły nacisku sanek na chodnik, która z kolei zgodnie z 3. zasadą dynamiki Newtona jest równa sile reakcji, z jaką chodnik działa na sanki.

Siłę tarcia F_t zapiszemy więc:
\[F_t = Nf_d\tag{4}\]
Siłę reakcji N obliczymy z równania (3):
\[N \,=\, mg - T\sin\varphi\tag{5}\]
Z równań (4) i (5):
\[F_{t} \,=\, f_{d}\left(mg - T\sin\varphi\right)\tag{6}\]
Po podstawieniu równania (6) do równania (2) możemy składowe sił dla osi x zapisać jako:
\[T\cos\varphi - f_{d}\left(mg - T\sin\varphi\right) \,=\, 0\tag{7}\]
Z równania (7) pozostaje wyznaczyć siłę ciągu:
\[T \,=\, \frac{mgf_{d}}{\cos\varphi + f_{d}\sin\varphi}\tag{8}\]
Do równania (8) podstawiamy dane:
\[T \,=\, \frac{20\cdot{9{,}81}\cdot{0{,}1}}{\cos 30^{\circ} + 0{,}1\cdot\sin30^{\circ}}\,\mathrm{N} \,=\,\frac{19{,}62}{\frac{\sqrt{2}}{2} + 0{,}1\cdot{0{,}5}}\,\mathrm{N}\] \[T\,=\,21{,}4\,\mathrm{N}\]
Odpowiedź: Wartość siły ciągu T, z jaką dziewczynka ciągnie sanki, wynosi 21,4 N.
ROZWIĄZANIE LICZBOWE CZĘŚCI 3 - wartość siły reakcji
Siła reakcji N, którą chodnik działa na sanki, dana jest wzorem (5):
\[N \,=\, mg - T\sin\varphi\tag{5}\]
Podstawmy za T wyrażenie ze wzoru (7):
\[N \,=\, mg - \frac{mgf_{d}}{\cos\varphi + f_{d}\sin\varphi}\sin\varphi \,=\, mg \left(1 - \frac{f_{d}\sin\varphi}{\cos\varphi + f_{d}\sin\varphi}\right)\,=\,\] \[\,=\, mg\left(\frac{\cos\varphi}{\cos\varphi + f_{d}\sin\varphi}\right) \,=\, mg\left(\frac{1}{1 + f_{d}\tan\varphi}\right)\tag{9}\]
Podstawmy dane do równania (9):
\[N \,=\, 20{\cdot}9{,}81\left(\frac{1}{1 + 0{,}1\tan30^{\circ}}\right)\,\textrm{N}\,=\, 196{,}2\left(\frac{1}{1 + 0{,}1\frac{\sqrt{3}}{3}}\right)\,\mathrm{N}\] \[N\,=\,185{,}5\,\mathrm{N}\]
Odpowiedź: Wartość siły reakcji N, którą chodnik działa na sanki, wynosi 185,5 N.
ROZWIĄZANIE LICZBOWE CZĘŚCI 4 - wartość siły tarcia
Siła tarcia F_t dana jest wyrażeniem (4):
\[F_{t} \,=\, Nf_d\tag{4}\]
Podstawmy do równania (4) N z równania (9), otrzymamy:
\[F_{t} \,=\, mg\left(\frac{1}{1 + f_d\tan{\varphi}}\right)f_d\tag{10}\]
Do równania (10) podstawmy dane:
\[F_t\,=\, 20\cdot {9{,}81}\left(\frac{1}{1 + 0{,}1\,\tan{30^{\circ}}}\right)0{,}1\,\mathrm{N}\,=\, 19{,}62\,\left(\frac{1}{1 + 0{,}1\frac{\sqrt{3}}{3}}\right)\,\mathrm{N}\] \[F_t\,=\,18{,}6\,\mathrm{N}\]
Odpowiedź: Wartość siły tarcia F_t działającej na sanki wynosi 18,6 N.
PEŁNA ODPOWIEDŹ

1) Przyspieszenie sanek a wynosi zero.

2) Wartość siły ciągu, którą dziewczynka działa na sanki wynosi

\[T \,=\, \frac{mgf_{d}}{\cos{\varphi} + f_{d}\sin{\varphi}}\,=\,21{,}4\,\mathrm{N}.\]

3) Wartość siły nacisku sanek na chodnik wynosi

\[N \,=\, mg\left(\frac{1}{1 + f_{d}\tan{\varphi}}\right)\,=\,185{,}5\,\mathrm{N}.\]

4) Wartość siły tarcia działającej na sanki wynosi

\[F_{t} \,=\, mg\left(\frac{1}{1 + f_{d}\tan{\varphi}}\right)f_{d}\,=\,18{,}6\,\mathrm{N}.\]