Łódka
Kod zadania: 733
Zapis
\(v=4 \mathrm{km\cdot h^{-1}}\) prędkość łódki względem wody \(r=1{,}6 \mathrm{km\cdot h^{-1}}\) prędkość prądu rzeki \(t\) czas potrzebny na przepłynięcie z miasta A do B i z powrotem \(t'\) czas potrzebny na przepłynięcie tej samej odległości po jeziorze \(\frac{t}{t'}\,=\,\mathrm{?}\) Podpowiedź 1: Prędkość, z jaką płynie łódka z miasta A do miasta B
Narysuj obrazek pokazujący ruch łódki i zaznacz na nim obie prędkości, czyli prędkość łódki względem rzeki i prędkość prądu w rzece.
Wyznacz prędkość łódki względem brzegu. Zastanów się, w jakim czasie łódka pokona odległość między miastami A i B.
Podpowiedź 2: Prędkość, z jaką łódka płynie z miasta B do miasta A
Narysuj obrazek pokazujący ruch łódki z miasta b do miasta A i zaznacz prędkość łódki względem rzeki oraz prędkość nurtu rzeki. Wyznacz prędkość łódki względem brzegu. Następnie wyznacz czas, w którym łódka przepłynie odległość między miastami B i A.Podpowiedź 3: Wyznaczenie czasu
Wyznacz czas potrzebny przepłynięcie przez łódkę odległości 2AB z prędkością v.CAŁE ROZWIĄZANIE
Zakładamy, że odległość między miastami A i B wynosi s km.
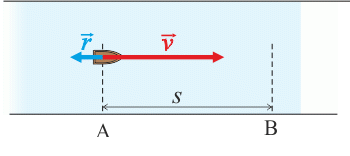
Prędkość łódki względem brzegu można obliczyć jako różnicę prędkości łódki względem wody i prędkości prądu rzeki:
\[v_1\,=\,v-r\,.\]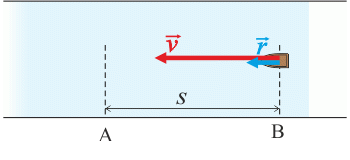
Prędkość łódki względem brzegu tym razem jest sumą prędkości łódki względem rzeki i prędkości prądu rzeki:
\[v_2\,=\,v+r\,.\]Łódka płynąc pod prąd pokona odległość między miastami A i B w czasie:
\[t_1\,=\,\frac{s}{v_1}\,=\,\frac{s}{v-r}\,.\]a płynąc z prądem w czasie:
\[t_2\,=\,\frac{s}{v_2}\,=\,\frac{s}{v+r}\,.\]Czas potrzebny na pokonanie odległość z miasta A do B i z powrotem wynosi:
\[t\,=\,t_1+t_2\,=\,\frac{s}{v-r}+\frac{s}{v+r}\,=\,s\,\left(\frac{1}{v-r}+\frac{1}{v+r}\right)\,=\,\frac{2v}{v^{2}-r^{2}}\,s\,.\]Na jeziorze łódka przepłynie odległość 2s z prędkością v w czasie:
\[t'\,=\,\frac{s}{v}+\frac{s}{v}\,=\,\frac{2}{v}s\,.\]Stosunek t/t' jest równy:
\[\frac{t}{t'}\,=\,\frac{\frac{2v}{v^{2}-r^{2}}\,s}{\frac{2}{v}\,s}\,=\,\frac{v^{2}}{v^{2}-r^{2}}\,=\,\frac{1}{1-\frac{r^{2}}{v^{2}}}\,.\]Podstawiamy wartości liczbowe:
\[\frac{t}{t'}\,=\,\frac{4^{2}}{4^{2}-1{,}6^{2}}\,=\,\frac{16}{13{,}44}\,\dot=\,1{,}19\,.\]Odpowiedź
Stosunek czasu potrzebnego na przepłynięcie odległości 2AB na rzece i po jeziorze jest równy:
\[\frac{t}{t'}\,=\,\frac{\frac{2v}{v^{2}-r^{2}}\,s}{\frac{2}{v}\,s}\,=\,\frac{v^{2}}{v^{2}-r^{2}}\,=\,\frac{1}{1-\frac{r^{2}}{v^{2}}}\,.\]Po obliczeniu otrzymujemy wartość:
\[\frac{t}{t'}\,=\,\frac{4^{2}}{4^{2}-1{,}6^{2}}\,=\,\frac{16}{13{,}44}\,\dot=\,1{,}19\,.\]Uwaga:
Mimo, że wydaje się, że łódka płynąc po rzece raz z prądem raz pod prąd nie powinna tracić na czasie przepłynięcia, podróż po rzece zajmuje więcej czasu niż przepłynięcie tej samej odległości tam i z powrotem po jeziorze.
Wynik liczbowy jest niezwykle ciekawy: ten sam czynnik, \({1-\frac{v^{2}}{c^{2}}}\) występuje w skróceniu odległości (i wydłużeniu czasu) w szczególnej teorii względności Einsteina.

