Tocząca się kulka
Kod zadania: 1101
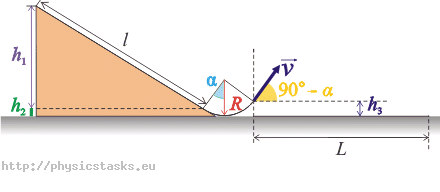
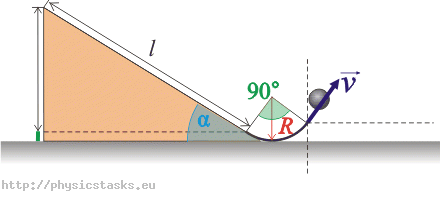
Kulka stoczyła się z równi o długości l = 2 m , ustawionej pod kątem α = 30° do poziomu i zakończonej łukiem o promieniu R = 0,4 m i kącie rozwarcia 90° (patrz rysunek).
Szybkość, z jaką kulka opuściła tor, miała wartość v = 3,5 m·s−1 .
a) Określ maksymalną wysokość H, na którą wzniesie się kulka po opuszczeniu toru.
b) Określ czas T , w którym kulka znajduje się w powietrzu po opuszczeniu toru.
c) Określ zasięg L od miejsca opuszczenia toru do miejsca, w którym kulka spadnie.
Zapis danych
l = 2 m długość równi α = 30° kąt nachylenia równi R = 0,4 m promień łuku v = 3,5 m·s−1 szybkość, z którą kulka opuszcza tor H = ? (m) maksymalna wysokość, na którą wzniesie się kulka T = ? (s) czas, w którym kulka znajduje się w powietrzu L = ? (m) odległość, w której kulka spadnie Z tablic g = 9,81 m·s−2 przyspieszenie grawitacyjne Podpowiedź 1: Pomocniczy rysunek
Jak opiszesz ruch kulki po opuszczeniu toru?
Narysuj pomocniczy rysunek i zaznacz na nim wielkości potrzebne w rozwiązaniu.
Zapisz wszystkie związki między wielkościami, wynikające z rysunku.
Podpowiedź 2 do a): Maksymalna wysokość
Jakie związki (dla współrzędnych i składowych prędkości) możemy zapisać dla rzutu ukośnego w górę z prędkością początkową v i pod kątem 90° − α?
Jak z tych związków określisz maksymalną wysokość, na jaką wzniesie się kulka po opuszczeniu toru?
Podpowiedź 3 do b): Czas lotu kulki
Całkowity czas, w którym kulka znajduje się w powietrzu, składa się z czasu wznoszenia i czasu spadania kulki.
Jak te czasy obliczysz?
Podpowiedź 4 do c): Długość (zasięg) lotu
Poziomą odległość od miejsca, w którym kulka opuści tor do miejsca jej spadku oznacz L i określ ją na podstawie rysunku.
Jak ją obliczysz?
PEŁNE ROZWIĄZANIE:
a) Wysokość maksymalna
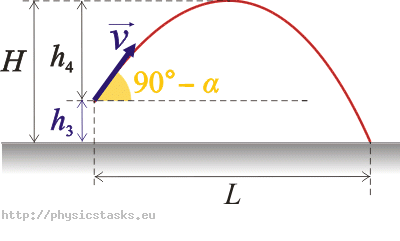
Mamy tu do czynienia z rzutem ukośnym w górę z wysokości początkowej h3 pod kątem 90° − α z prędkością początkową \(\vec{v}\) (patrz rysunek 1).
Rysunek 1:
Rysunek 2:
Z rysunków 1,2 wynikają związki kąta α z danymi wielkościami:
\[h_1\,=\,l\sin\alpha\,,\] \[h_2\,=\,R\left(1\,-\,\cos\alpha\right)\,,\] \[h_3\,=\,R\left[1\,-\,\cos(90^{\circ}-\alpha)\right]\,=\,R\left(1\,-\,\sin\alpha\right)\,,\] \[H\,=\,h_3\,+\,h_4\,.\]Dla rzutu ukośnego w górę z prędkością początkową v pod kątem 90° − α otrzymujemy:
\[v_x\,=\,v\,\cos(90^{\circ}-\alpha)\,=\,v\,\sin\alpha\,,\] \[v_y=v\sin(90^{\circ}-\alpha)-gt=v\cos\alpha-gt\,,\] \[x\,=\,vt\,\sin\alpha\,,\] \[y\,=\,vt\,\cos\alpha\,-\,\frac{1}{2}gt^{2}\,.\]Dla maksymalnej wysokości:
\[v_y\,=\,0\,,\] \[t_v\,=\,\frac{v\,\cos\alpha}{g}\,,\] \[h_4\,=\, vt_v\,\cos\alpha\,-\,\frac{1}{2}gt_v^{2} \,=\, \frac{v^{2}\,\cos^{2}\alpha}{g}\,-\,\frac{gv^{2}\,\cos^{2}\alpha}{2g^{2}}\,=\,\frac{v^{2}\,\cos^{2}\alpha}{2g}\,,\] \[H \,=\, h_3 \,+\, h_4 \,=\, R\,\left(1\,-\,\sin\alpha\right)\,+\,\frac{v^{2}\,\cos^{2}\alpha}{2g}\,.\]Podstawiając dane liczbowe:
\[H\,=\,\left[0{,}4\,\left(1\,-\,\frac{1}{2}\right)\,+\,\frac{3{,}5^{2}\cdot \left(\frac{\sqrt{3}}{2}\right)^{2}}{2{\cdot} 9{,}81}\right]\,\mathrm{m}\,,\] \[H\,\dot=\,0{,}67\,\mathrm{m}\,.\]b) Czas lotu
Czas wznoszenia się:
\[t_v\,=\,T_1\,=\,\frac{v\,\cos\alpha}{g}\,.\]Czas spadania (spadek swobodny z wysokości H):
\[H\,=\,\frac{1}{2}gT_2^{2}\,,\] \[T_2\,=\,\sqrt{\frac{2H}{g}}\,.\]Całkowity czas lotu:
\[T\,=\,T_1\,+\,T_2\,=\,\frac{v\,\cos\alpha}{g}\,+\,\sqrt{\frac{2H}{g}}\,.\]Po podstawieniu danych liczbowych:
\[T\,=\,\left[\frac{3{,}5\cdot\frac{\sqrt{3}}{2}}{9{,}81}\,+\,\sqrt{\frac{2{\cdot} 0{,}67}{9{,}81}}\right]\,\mathrm{s}\,,\] \[T\,\dot=\,0{,}68\,\mathrm{s}\,.\]c) Zasięg lotu
W kierunku poziomym kulka porusza się ruchem jednostajnym z prędkością vsinα w czasie T.
Zasięg L liczony od punktu, w którym kulka opuszcza tor wynosi:
\[L\,=\,vT\,\sin\alpha\,.\]Po podstawieniu danych liczbowych:
\[L=\left(3{,}5{\cdot} 0{,}68\cdot \frac{1}{2}\right)\,\mathrm{m}\,,\] \[L\,\dot=\,1{,}19\,\mathrm{m}\,.\]Odpowiedź
a) Na maksymalną wysokość, do której doleci kulka po opuszczeniu toru, otrzymujemy:
\[H\,=\,R\left(1\,-\,\sin\alpha\right)\,+\,\frac{v^{2}\,\cos^{2}\alpha}{2g}\,\dot=\,0{,}67\,\mathrm{m}\,.\]b) Czas, w którym kulka znajduje się w powietrzu wynosi:
\[T\,=\,T_1\,+\,T_2\,=\,\frac{v\,\cos\alpha}{g}\,+\,\sqrt{\frac{2H}{g}}\,\dot=\,0{,}68\,\mathrm{s}\,.\]c) Zasięg rzutu od miejsca, w którym kulka opuści tor wynosi:
\[L\,=\,vT\,\sin\alpha\,\dot=\,1{,}19\,\mathrm{m}\,.\]