Wąż ogrodowy
Kod zadania: 1103
Strumieniem wody tryskającym z węża ogrodowego z prędkością początkową 15 m·s−1 chcemy dosięgnąć jak najwyżej, kierując go na pionową ścianę odległą o 10 m od dyszy.
a) Jaki powinniśmy wybrać kąt początkowy?
b) Do jakiej wysokości na ścianie dotrze woda?
c) Pod jakim kątem woda uderzy w ścianę? Określ odchylenie od poziomu wektora prędkości chwilowej wody w momencie trafienia w ścianę.
Opór powietrza zaniedbujemy.
Zapis danych
v0 = 15 m·s−1 prędkość początkowa strumienia wody d = 10 m odległość ściany α = ? (°) kąt początkowy h = ? (m) maksymalna wysokość, do której sięgnie woda ψ = ? (°) kąt, pod którym woda trafia w ścianę Z tablic: g = 9,81 m·s−2 przyspieszenie grawitacyjne Analiza
Chcemy ustalić, pod jakim kątem α musimy skierować wąż, aby woda dotarła jak najwyżej; powinniśmy najpierw ustalić, jak ta wysokość h zależy od kąta α. Inaczej mówiąc, szukamy maksimum funkcji h(α).
Zwróćmy úwagę, że maksymalna wysokość na ścianie wcale nie musi odpowiadać maksymalnej wysokości rzutu dla danego kąta α. Trzeba sobie uświadomić, że to odległość ściany jest ustalona. Pomyśl o różnych możliwych sytuacjach.
Podpowiedź 1 do a): Pomocniczy rysunek, rodzaj ruchu
Naszkicuj pomocniczy rysunek. O jaki rodzaj ruchu chodzi? Jak będzie się zmieniać z czasem x-owa i y-owa współrzędna prędkości wody? Jak się będzie zmieniać x-owa i y-owa współrzędna położenia?
Podpowiedź 2 do a): Czas dolotu wody do ściany, wysokość
Jak długo trwać będzie lot wody do ściany dla danego kąta α? Jaka wysokość h w miejscu uderzenia strumienia wody w ścianę odpowiada temu czasowi?
Podpowiedź 3 do a): Kąt początkowy α
Chcielibyśmy wiedzieć, dla jakiego kąta α wysokość h miejsca uderzenia strumienia wody na ścianie będzie maksymalna. Szukamy więc maksimum funkcji h = h(α). Jaki jest na to matematyczny sposób?
Podpowiedź 4 do b): Maksymalna wysokość wody na ścianie
Znamy już kąt odpowiadający maksymalnej wysokości wody na ścianie i zależność tej wysokości h od kąta α. Maksymalną wysokość możemy już łatwo obliczyć.
Podpowiedź 5 do c): Kąt ψ uderzenia wody w ścianę
Przedstaw na rysunku wektor prędkości wody w chwili uderzenia w ścianę i jego składowe w kierunku osi x i y. Za ich pomocą można łatwo określić szukany kąt. Wartości obu składowych prędkości w chwili uderzenia w ścianę oblicz na podstawie równań (1) i (2) z Podpowiedzi 1.
PEŁNE ROZWIĄZANIE
a) kąt początkowy
Rysunek 1:
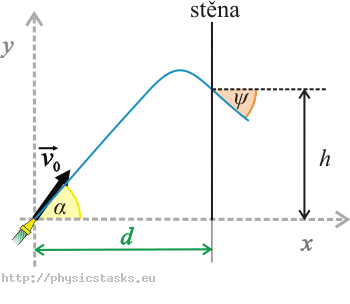
Początek układu współrzędnych umieszczamy w dyszy węża.
Mamy do czynienia z rzutem ukośnym w górę.
X-owa i y-owa składowa prędkości wody oraz x-owa i y-owa składowa położenia zmienia się w czasie według wzorów:
\[v_x\,=\,v_0\,\cos\alpha\tag{1}\] \[v_y\,=\,v_0\,\sin\alpha\,-\,gt\tag{2}\]
\[x\,=\,v_0t\,\cos\alpha\tag{3}\] \[y\,=\,v_0t\,\sin\alpha\,-\,\frac{1}{2}gt^{2}\tag{4}\]Na czas lotu wody i wysokość miejsca uderzenia w ścianę zapiszemy: \(x\,=\,d\)
Podstawmy z (3):
\[d\,=\,v_0t\,\cos\alpha\] \[t\,=\,\frac{d}{v_0\,\cos\alpha}\tag{5}\]
\[y\,=\,h\]Podstawmy z (4):
\[h\,=\,v_0t\,\sin\alpha\,-\,\frac{1}{2}gt^{2}\]Podstawmy jeszcze za t z (5):
\[h\,=\,d\,\mathrm{tg}\alpha\,-\,\frac{gd^{2}}{2v_0^{2}\,\cos^{2}\alpha}\,=\,d\mathrm{tg}\alpha\,-\,\frac{gd^{2}}{2v_0^{2}}\,\left(1\,+\,\mathrm{tg}^{2}\alpha \right)\tag{6}\]Szukamy takiej wartości kąta α, dla której wysokość h miejsca uderzenia wody jest maksymalna; inaczej - szukamy ekstremum funkcji h = h(α).
Sprawdźmy, w jakim przypadku pochodna funkcji h względem α jest równa zeru:
\[\frac{\mathrm{d}h}{\mathrm{d}\alpha}\,=\,\frac{\mathrm{d}}{\mathrm{d}\alpha}\left(d\,\mathrm{tg}\alpha\,-\,\frac{gd^{2}}{2v_0^{2}\,\cos^{2}\alpha}\right)\] \[\frac{\mathrm{d}h}{\mathrm{d}\alpha}\,=\,\frac{d}{\cos^{2}\alpha}\,-\,\frac{gd^{2}\sin\alpha}{v_0^{2}\cos^{3}\alpha}\,=\,\frac{d}{\cos^{2}\alpha}\left(1\,-\,\frac{gd}{v_0^{2}}\,\mathrm{tg}\alpha\right)\,=\,0\] \[1\,-\,\frac{gd}{v_0^{2}}\,\mathrm{tg}\alpha \,=\, 0\] \[\mathrm{tg}\alpha\,=\,\frac{v_0^{2}}{gd}\tag{7}\]Dla kąta początkowego \[\alpha\,=\,\mathrm{arctg}\,\frac{v_0^{2}}{gd}\] funkcja h(α) osiąga maksimum.
Dla zadanych wartości liczbowych:
\[\mathrm{tg}\alpha\,=\,\frac{15^{2}}{9{,}81{\cdot}10} \,\dot=\, 2{,}294\] \[\alpha\,=\,\mathrm{arctg}\,2{,}294\,\,\dot=\,\,66{,}4^{\circ}\]b) Wysokość miejsca uderzenia
Wiemy już, że wysokość miejsca uderzenia w ścianę określa wzór (6):
\[h\,=\,d\mathrm{tg}\alpha\,-\,\frac{gd^{2}}{2v_0^{2}\cos^{2}\alpha}\,=\,d\mathrm{tg}\alpha\,-\,\frac{gd^{2}}{2v_0^{2}}\left(1\,+\,\mathrm{tg}^{2}\alpha\right)\,.\tag{6}\]Wiemy też, że wysokość h miejsca uderzenia będzie największa dla kąta α określonego wzorem (7):
\[\mathrm{tg}\alpha\,=\,\frac{v_0^{2}}{gd}\,.\tag{7}\]Po podstawieniu (7) do (6) otrzymamy:
\[h\,=\,\frac{dv_0^{2}}{gd}\,-\,\frac{gd^{2}}{2v_0^{2}}\left(1\,+\,\frac{v_0^{4}}{g^{2}d^{2}}\right)\,=\,\frac{v_0^{2}}{2g}\,-\,\frac{gd^{2}}{2v_0^{2}}\,.\]Dla podanych wartości liczbowych:
\[h\,=\,\left(\frac{15^{2}}{2{\cdot}9{,}81}\,-\,\frac{9{,}81{\cdot}10^{2}}{2{\cdot}15^{2}}\right)\,\mathrm{m}\] \[h\,\dot=\,9{,}29\,\mathrm{m}\]c) odchylenie ψ od poziomu kierunku wektora prędkości wody w chwili uderzenia w ścianę
Na rysunku zaznaczmy wektor prędkości wody w chwili uderzenia, jego składowe i szukany kąt.
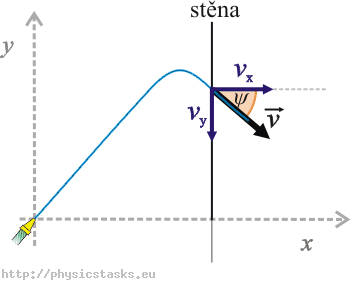
Odchylenie ψ od poziomu kierunku wektora prędkości wody w chwili uderzenia w ścianę określimy ze wzoru:
\[\mathrm{tg}\psi\,=\,\frac{v_y}{v_x}\,.\]Za vx i vy podstawimy wyrażenia ze wzorów (1) i (2), za czas t wyrażenie ze wzoru (5):
\[\mathrm{tg}\psi\,=\,\frac{v_0\,\sin\alpha\,-\,gt}{v_0\cos\alpha}\,=\,\mathrm{tg}\alpha\,-\,\frac{gd}{v_0^{2}\cos^{2}\alpha}\,.\]Przekształcimy korzystając z (7):
\[\mathrm{tg}\psi\,=\,\mathrm{tg}\alpha\,-\,\frac{1}{\mathrm{tg}\alpha\cos^{2}\alpha}\] \[\mathrm{tg}\psi\,=\,\mathrm{tg}\alpha\,-\,\frac{1}{\sin\alpha\cos\alpha}\,=\,\frac{\sin^{2}\alpha\,-\,1}{\sin\alpha\cos\alpha}\,=\,-\,\frac{1}{tg\alpha}\,=\, -\,\frac{gd}{v_0^{2}}\]Podstawiając dane liczbowe:
\[\mathrm{tg}\psi\,=\,-\frac{9{,}81{\cdot}10}{15^{2}} \,\dot=\, -0{,}436\] \[\psi\,\dot=\,-\,23{,}6^{\circ}\]Kąt odchylenia ψ kierunku wektora prędkości wody od poziomu ma wartość ujemną. Patrz rysunek.
Uwaga:
Przy maksymalnej wysokości na torze lotu wody składowa y-owa prędkości wynosi zero, a wówczas i kąt φ jest zerowy.
Odpowiedź
a) Aby dosięgnąć strumieniem wody jak najwyżej na pionową ścianę, musimy skierować strumień pod kątem początkowym α , dla którego:
\[\alpha\,=\,\mathrm{arctg}\,\frac{v_0^{2}}{gd}\,\dot=\,66{,}4^{\circ}\,.\]b) Strumień wody sięgnie do wysokości h, dla której:
\[h\,=\,\frac{v_0^{2}}{2g}\,-\,\frac{gd^{2}}{2v_0^{2}}\,\dot=\,9{,}29\,\mathrm{m}\,.\]c) Woda uderzy w ścianę pod kątem ψ , dla którego:
\[\mathrm{tg}\psi\,=\,-\,\frac{gd}{v_0^{2}}\,.\]Dla zadanych wartości liczbowych:
\[\psi\,=\,-\,23{,}6^{\circ}\]




