Koszykarz
Kod zadania: 1102
Obręcz kosza na boisku do koszykówki znajduje się na wysokości h1 nad podłogą. Środek kosza znajduje się w odległości L od linii rzutów wolnych. Koszykarz wykonuje rzuty wolne, piłka opuszcza rękę w miejscu, gdzie jej centrum jest dokładnie nad linią rzutów wolnych na wysokości h2 nad podłogą.
Określimy kąt optymalny α jako taki kąt, przy którym środek piłki przechodzi przez środek obręczy, a ponadto piłce nadajemy najmniejszą możliwą prędkość początkową. Udowodnij, że wartość tego kąta określona jest wzorem α = 45˚ + β/2, gdzie β to tzw. kąt obserwacji , tj. odchylenie od płaszczyzny linii łączącej punkt zaczepienia obręczy z punktem początkowym rzutu.
Wyznacz kąt optymalny dla zadanych wielkości oraz odpowiednią wartość prędkości początkowej piłki.
Zaniedbujemy opór powietrza.
Wykonaj obliczenia dla: h1 = 3,05 m, L = 5,425 m, h2 = 2,45 m, g = 9,81 m·s-2 .
Zapis danych
h1 = 3,05 m wysokość obręczy kosza nad podłogą L = 5,425 m pozioma odległość środka kosza od linii rzutów wolnych h2 = 2,45 m wysokość środka piłki nad podłogą w momencie, gdy środek piłki leży dokładnie nad linią rzutów wolnych α = ? kąt optymalny v0 = ? (m·s−1)
wartość prędkości początkowej piłki odpowiednia dla kąta optymalnego Z tablic: g = 9,81 m·s−2
przyspieszenie grawitacyjne
Podpowiedź 1: Pomocniczy rysunek
Naszkicuj pomocniczy rysunek, zaznaczając kąt optymalny i kąt obserwacji, odległość L i wysokość obręczy kosza nad miejscem wyrzucenia piłki.
Podpowiedź 2: Ruch piłki w kierunku poziomym i pionowym
Jakim ruchem porusza się piłka w kierunku poziomym? Jakim w kierunku pionowym?
Podpowiedź 3: Prędkość piłki w kierunku poziomym i pionowym
Jaka jest pozioma prędkość piłki i jak zmienia się w czasie x-owa składowa jej położenia?
Jaka jest pionowa prędkość piłki i jak zmienia się w czasie y-owa składowa jej położenia?
Jakie wartości będą mieć współrzędne x i y w chwili, gdy piłka doleci do obręczy kosza? Zapisz odpowiednie wzory i wyznacz z nich kwadrat początkowej prędkości v02(skorzystaj też ze związku tgβ = H/L).
Podpowiedź 4: Minimalna wartość wyrażenia
Dla jakiego kąta α wartość wyrażenia v02 będzie minimalna?
Podpowiedź 5: Prędkość początkowa dla kąta optymalnego
Określ prędkość początkową v0 dla kąta optymalnego α, a więc w przypadku, gdy sin(2α−β) = 1. Sinus i cosinus kąta β można wyrazić poprzez odległości H i L.
PEŁNE ROZWIĄZANIE
Oznaczmy przez L i H poziomą i pionową odległość środka obręczy od punktu początkowego, α kąt optymalny, β kąt obserwacji, t czas lotu, v0 prędkość początkowa piłki, v prędkość piłki w chwili wpadania do kosza (patrz rysunek 1,2).
Rysunek 1:
\[H = h_1 - h_2\]
Rysunek 2:
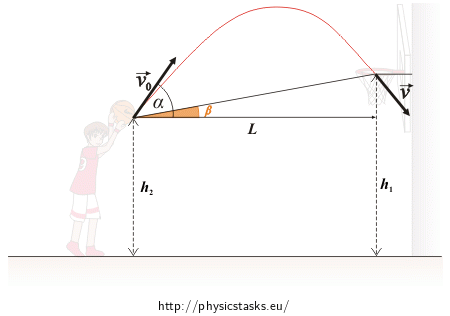
W kierunku poziomym piłka porusza się ruchem jednostajnym. W kierunku pionowym ruch piłki opisujemy jako rzut pionowy w górę.
Będziemy mieli:
\[v_x=v_0\cos\alpha\,,\] \[v_y=v_0\sin\alpha-gt\,,\] \[x=v_0t\cos\alpha\,,\] \[y=v_0t\sin\alpha-\frac{1}{2}gt^{2}\,.\]W chwili, gdy piłka doleci do obręczy kosza:
\[x=L=v_0t\cos\alpha\,.\]Stąd:
\[t=\frac{L}{v_0\cos\alpha}\,,\] \[y=H=v_0t\sin\alpha-\frac{1}{2}gt^{2}=Ltg\alpha-\frac{gL^{2}}{2v_0^{2}\cos^{2}\alpha}\,.\]I dalej:
\[\frac{gL^{2}}{2v_0^{2}\cos^{2}\alpha} = Ltg\alpha- H\,,\] \[\frac{gL^{2}}{Ltg\alpha- H} = 2v_0^{2}\cos^{2}\alpha\,,\] \[v_0^{2}=\frac{gL^{2}}{2(Ltg\alpha-H)\cos^{2}\alpha}=\frac{gL^{2}}{2(L\sin\alpha\cos\alpha-Hcos^{2}\alpha)}\,.\]Po podstawieniu \(H=Ltg\beta\) i przekształceniach otrzymujemy:
\[v_0^{2}=\frac{gL^{2}}{2(L\sin\alpha\cos\alpha-Ltg\beta\cos^{2}\alpha)}=\frac{gL}{sin2\alpha-tg\beta(1+\cos2\alpha)}\,,\] \[v_0^{2}=\frac{gL\cos\beta}{\sin2\alpha\cos\beta-\sin\beta-\sin\beta\cos2\alpha}=\frac{gL\cos\beta}{\sin(2\alpha-\beta)-\sin\beta}\,.\]Uwaga: W przekształceniach korzystamy ze wzorów trygonometrycznych:
\[2\sin\alpha\cos\alpha = \sin2\alpha\,,\] \[\cos2\alpha = cos^{2}\alpha - sin^{2}\alpha\,,\] \[\sin(2\alpha-\beta) = sin2\alpha\cos\beta - cos2\alpha\sin\beta\,.\]Wartość wyrażenia będzie najmniejsza, gdy mianownik osiągnie wartość maksymalną, czyli dla:
\[\sin(2\alpha-\beta)=1\,,\] \[2\alpha-\beta=90^{\circ}\,.\]Skąd:
\[\alpha=45^{\circ}+\frac{\beta}{2}\,.\]W takim przypadku:
\[v_0^{2}=\frac{gL\cos\beta}{1-\sin\beta}\,.\]Będziemy mieli:
\[\cos\beta = \frac{L}{\sqrt{H^{2}+L^{2}}}\,, \] \[\sin\beta = \frac{H}{\sqrt{H^{2}+L^{2}}}\,. \]Podstawmy \(H = h_1 - h_2\) :
\[\cos\beta = \frac{L}{\sqrt{(h_1 - h_2)^{2}+L^{2}}}\,, \] \[\sin\beta = \frac{h_1 - h_2}{\sqrt{(h_1 - h_2)^{2}+L^{2}}}\,.\]Wtedy:
\[v_0^{2}=\frac{\frac{gL^{2}}{\sqrt{H^{2}+L^{2}}}}{1-\frac{H}{\sqrt{H^{2}+L^{2}}}}=\frac{gL^{2}}{\sqrt{H^{2}+L^{2}}-H}=g\left(\sqrt{H^{2}+L^{2}}+H\right)\,.\]Podstawmy \(H = h_1 - h_2\) :
\[v_0^{2}=g\left(\sqrt{(h_1 - h_2)^{2}+L^{2}}+(h_1 - h_2)\right)\,.\]Dla zadanych wartości liczbowych:
\[\sin\beta = \frac{3{,}05-2{,}45}{\sqrt{(3{,}05 - 2{,}45)^{2}+5{,}425^{2}}}\] Stąd wynika: \(\beta\dot{=}6^{\circ}\) Wówczas: \[\alpha=45^{\circ}+\frac{\beta}{2}\,,\] \[\alpha\dot{=}48^{\circ}\,.\] I dalej: \[v_0^{2}=9{,}81\left(\sqrt{(3{,}05 - 2{,}45)^{2}+5{,}425^{2}}+(3{,}05 - 2{,}45)\right)\,\mathrm{m^{2}.s^{-2}}\,,\] \[v_0\dot{=}7{,}7\,\mathrm{m.s^{-1}}\,.\]Odpowiedź
Kąt optymalny dla rzutu wynosi:
\(\alpha=45^{\circ}+\frac{\beta}{2}\) , gdzie \(\sin\beta = \frac{h_1 - h_2}{\sqrt{(h_1 - h_2)^{2}+L^{2}}}\,. \)Dla zadanych wartości: \(\alpha\dot{=}48^{\circ}\,.\)
Odpowiednia wartość prędkości początkowej piłki wynosi:
\[v_0^{2}=g\left(\sqrt{(h_1 - h_2)^{2}+L^{2}}+(h_1 - h_2)\right)\,.\]Dla zadanych wartości:
\[v_0\dot{=}7{,}7\,\mathrm{m.s^{-1}}\,.\]



