Zbiór rozwiązanych zadań i problemów fizycznych

Samolot ratunkowy

Kod zadania: 1100

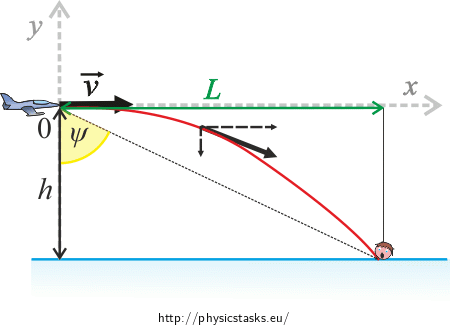
Samolot ratunkowy leci na pomoc tonącemu. Pilot utrzymuje stałą wysokość 1 200 m nad powierzchnią wody i kieruje się prosto nad głowę tonącego (patrz rysunek). Prędkość samolotu ma wartość 430 km·h⁻¹.

Przy jakiej wartości kąta widzenia pilot powinien uwolnić kamizelkę ratunkową, aby spadła ona jak najbliżej tonącego?

Zaniedbujemy opór powietrza.

• Zapis danych

  h = 1 200 m	wysokość samolotu nad powierzchią wody
  v = 430 km·h−1	prędkość samolotu
  ψ = ? (°)	kąt widzenia
  Z tablic:
  g = 9,81 m·s−2	przyspieszenie grawitacyjne

• Podpowiedź 1: Prędkość początkowa ładunku

  Jaka jest prędkość początkowa ładunku (kamizelki)?

• Rozwiązanie podpowiedzi 1

  Prędkość początkowa ładunku (kamizelki) jest taka sama jak prędkość samolotu. Ma więc wartość v.

• Podpowiedź 2: Czas spadania ładunku na powierzchnię wody

  Jakim ruchem poruszać się będzie w kierunku pionowym ładunek po uwolnieniu?

  Jak określić jego czas spadania  t  na powierzchnię wody, jeśli znamy wysokość  h , z której go wypuszczono?

• Rozwiązanie podpowiedzi 2

  Ponieważ zaniedbujemy opór powietrza, w kierunku pionowym ładunek będzie spadał swobodnie.

  Znając wysokość, z której ładunek uwalniamy, możemy łatwo określić jego czas spadania na powierzchnię wody. W kierunku osi y zapiszemy:

  \[-h\,=\,-\,\frac{1}{2}gt^{2}\,,\]

  więc:

  \[h\,=\,\frac{1}{2}gt^{2}\,.\]

  (w kierunku osi y na ładunek działa tylko siła grawitacji).

  Przekształcając równanie określamy czas spadania t :

  \[t\,=\,\sqrt{\frac{2h}{g}}\,.\]

• Podpowiedź 3: Zasięg  L

  Jakim ruchem porusza się ładunek w kierunku poziomym?

  Jaki będzie zasięg L jego lotu w czasie t, kiedy to spadać będzie na powierzchnię wody? Czas spadania t określiliśmy w poprzedniej podpowiedzi.

• Rozwiązanie podpowiedzi 3

  W kierunku poziomym ładunek (i samolot) porusza się ruchem jednostajnym z prędkością v.

  Z rozwiązania poprzedniej podpowiedzi przypomnijmy wzór na czas t spadania ładunku na powierzchnię wody:

  \[t\,=\,\sqrt{\frac{2h}{g}}\,.\]

  W tym czasie poruszając się jednostajnie w kierunku poziomym ładunek uzyska zasięg:

  \[L\,=\,vt\,.\]

  Po podstawieniu wzoru na t otrzymujemy:

  \[L\,=\,v\,\sqrt{\frac{2h}{g}}\,.\]

• Podpowiedź 4: Kąt widzenia ψ

  Jak określisz wartość kąta widzenia ψ, przy którym pilot musi uwolnić ładunek tak, aby spadł on jak najbliżej tonącego?

  Spójrz na rysunek. Jaką funkcję trygonometryczną możesz wykorzystać w rozwiązaniu?

  Jakie wielkości będą potrzebne do obliczenia kąta widzenia ψ ? Czy je znamy?

• Rozwiązanie podpowiedzi 4

  Metodę obliczenia kąta widzenia ψ określimy w oparciu o rysunek.

  Skorzystamy z funcji trygonometrycznej tangens.

  Do obliczenia będzie nam potrzebny zasięg L , który w ruchu jednostajnym zależy od czasu spadania swobodnego t oraz wysokości, z której spada. Obie wielkości znamy.

   

  Mamy więc:

  \[\mathrm{tg}\psi\,=\,\frac{L}{h}\,=\,\frac{v\,\sqrt{\frac{2h}{g}}}{h}\,=\,v\,\sqrt{\frac{2}{hg}}\,.\]

  Po podstawieniu danych liczbowych:

  \[\mathrm{tg}\psi\,=\frac{430\, 000}{3\, 600}\sqrt{\frac{2}{1\, 200{\cdot}9{,}81}}\,\dot=\, 1{,}556\,,\] \[\psi\,=\,57^{\circ}\,.\]

   

  Uwaga: Prędkość pozioma ładunku w każdej chwili jest taka sama jak prędkość samolotu, pilot ma więc spadający ładunek cały czas pod sobą.

   

• PEŁNE ROZWIĄZANIE:

  Prędkość początkowa ładunku jest taka sama jak prędkość samolotu. Ma więc wartość \(v\).

  Ponieważ nie uwzględniamy oporu powietrza, ładunek spada w kierunku pionowym swobodnie (ruchem jednostajnie przyspieszonym).

  Ponieważ wiemy, na jakiej wysokości ładunek uwolniono, możemy określić czas jego spadania na powierzchnię wody. W kierunku osi y zapiszemy:

  \[-h\,=\,-\,\frac{1}{2}gt^{2}\,,\]

  więc:

  \[h\,=\,\frac{1}{2}gt^{2}\,.\]

  (w kierunku osi y na ładunek działa tylko siła grawitacji).

  Po przekształceniu wzoru otrzymujemy czas ruchu t :

  \[t\,=\,\sqrt{\frac{2h}{g}}\,.\]

   

  W kierunku poziomym ładunek (i samolot) porusza się ze stałą prędkością v.

  W czasie ruchu ładunek oddali się więc w kierunku poziomym na odległość:

  \[L\,=\,vt\,.\]

  Po podstawieniu za t otrzymujemy:

  \[L\,=\,v\sqrt{\frac{2h}{g}}\,.\]

   

  Metoda obliczenia kąta widzenia ψ wynika z rysunku.

  Skorzystamy z funkcji trygonometrycznej tangens.

  Do obliczenia powinniśmy znać odległość  L , na którą oddali się ładunek w czasie  t  spadania swobodnego oraz wysokość, z której spada. Obie wielkości znamy.

   

  Zachodzi:

  \[\mathrm{tg}\psi\,=\,\frac{L}{h}=\frac{v\sqrt{\frac{2h}{g}}}{h}=v\sqrt{\frac{2}{hg}}\,.\]

   

  Po podstawieniu wartości liczbowych:

  \[\mathrm{tg}\psi\,=\,\frac{430 \,000}{3\, 600}\sqrt{\frac{2}{1 \,200{\cdot}9{,}81}}\,\dot=\, 1{,}556\,,\] \[\psi\,=\,57^{\circ}\,.\]

   

  Uwaga: Prędkość pozioma ładunku jest w każdej chwili taka sama jak prędkość samolotu, tak więc pilot ma cały czas ładunek pod sobą.

   

• Odpowiedź

  Aby ładunek spadł jak najbliżej tonącego, pilot musi go uwolnić przy kącie widzenia ψ, dla którego:

  \[\mathrm{tg}\psi\,=\,v\,\sqrt{\frac{2}{hg}}\,\dot=\,1{,}556\,,\] \[\psi\,=\,57^{\circ}\,.\]