Wózek na torze powietrznym

Kod zadania: 889

Wózek na torze powietrznym ma masę m_v = 250 g i jest przyspieszany przez pociągnięcie za sznurek przerzucony przez bloczek. Porównaj wartości przyspieszenia wózka, w przypadku gdy

a) ciągniemy za sznurek siłą 0,1 N

b) zawiesimy na sznurku ciało o ciężarze 0,1 N

Opór powietrza oraz masy sznurka i bloczku pomijamy.

Uwaga: Tor powietrzny to urządzenie, na którym możliwy jest ruch wózka bez tarcia. Wdmuchiwany od dołu strumień powietrza unosi wózek.

Podpowiedź 1a
Naszkicuj rysunek zaznaczając siły działające na wózek w przypadku, gdy ciągniemy za sznurek siłą o wartości 0,1 N. Zapisz równanie ruchu dla wózka.
Rozwiązanie podpowiedzi 1a
Siły działające na wózek w przypadku a):

\(\vec{F}\)…siła, którą ręka działa na wózek za pośrednictwem sznurka

\(\vec{N}\)…siła działania strumienia powietrza na wózek

\(\vec{F}_{Gv}\)…siła ciężkości działająca na wózek

Równanie ruchu:
\[\vec{F}_{Gv}+\vec{N}+\vec{F}\,=\, m_v\vec{a_1}\tag{1}\]
\(m_v\)…masa wózka

\(\vec{a}_1\)…przyspieszenie wózka
Podpowiedź 2a
Równanie ruchu z punktu (1) zapisz skalarnie i wyprowadź wzór na przyspieszenie a₁.
Rozwiązanie podpowiedzi 2a
Aby zapisać równania ruchu skalarnie, wprowadźmy układ odniesienia. Oś x prowadzimy wzdłuż kierunku ruchu pojazdu. Oś y jest prostopadła do osi x.

Zapisujemy równania ruchu skalarnie:
\[x:\hspace{10px}F\,=\,m_{v} a_{1}\tag{2}\] \[y:\hspace{10px}N - F_{Gv} \,=\,0\tag{3}\]
Pojazd nie porusza się wzdłuż osi y, dlatego składowa pionowa siły wynosi zero.

Z równania (2) uzyskamy wartość przyspieszenia a₁:
\[ a_1\,=\,\frac{F}{m_v}\tag{5}\]
Podstawiając wartości liczbowe:
\[ a_1\,=\,\frac{0{,}1}{0{,}25}\,\mathrm{m\cdot s^{-2}}\,=\, 0{,}4\,\mathrm{m \cdot s^{-2}}\tag{6}\]
Podpowiedź 1b
Sporządź rysunek uwzględniający siły działające na pojazd i ciężarek. Zapisz równania ruchu dla pojazdu i ciężarka.
Rozwiązanie podpowiedzi 1b
Siły działające na wózek i ciężarek w przypadku b):

Wózek:

\(\vec{N}\)…siła którą strumień powietrza działa od spodu na wózek

\(\vec{F}_{Gv}\)…siła ciężkości wózka

\(\vec{T^{\prime}}\)…siła, z jaką ciężarek za pośrednictwem sznurka działa na wózek

Ciężarek:

\(\vec{F}_{Gz}\)…siła ciężkości

\(\vec{T}\)… siła, z jaką wózek za pośrednictwem sznurka działa na ciężarek

Równania ruchu:

Równanie ruchu dla wózka:
\[\vec{F}_{Gv}+\vec{N}+\vec{T^{\prime}}\,=\, m_v\vec{a}_2\tag{7}\]
Równanie ruchu dla ciężarka:
\[\vec{F}_{Gz}+\vec{T}\,=\,m_z\vec{a}_2\tag{8}\]
\(m_v\)…masa wózka

\(m_z\)…masa ciężarka

\(\vec{a}_2\)…przyspieszenie wózka i ciężarka
Podpowiedź 2b
Równania ruchu (7) i (8) zapisz skalarnie. Zastanów się, co możemy powiedzieć o siłach naciągu sznurka T i T'.
Rozwiązanie podpowiedzi 2b
Aby równania ruchu zapisać skalarnie, wprowadzimy układ odniesienia. Oś x prowadzimy wzdłuż kierunku ruchu wózka (i dalej ciężarka). Oś y jest prostopadła do osi x.

Równania ruchu skalarnie:

Równanie ruchu wózka:
\[x:\hspace{10px}T^{\prime}\,=\,m_{v}a_2\tag{9}\] \[y:\hspace{10px}N - F_{Gv}\,=\,0\tag{10}\]
Wózek nie porusza się wzdłuż osi y, dlatego suma sił pionowych wynosi zero.

Równanie ruchu ciężarka:
\[x:\hspace{10px}F_{Gz}-T\,=\,m_{z}a_2\tag{11}\]
Ponieważ zaniedbujemy masę bloczka (a co za tym idzie - jego moment bezwładności), możemy w oparciu o 3. zasadę dynamiki Newtona zapisać:
\[|\vec{T}| \,=\, |\vec{T^{\prime}}|\]
Przepiszmy równanie (9):
\[T\,=\,m_{v}a_2\tag{12}\]
Podpowiedź 3b
Korzystając z równań (11) i (12) określ wartość przyspieszenia a₂.
Rozwiązanie podpowiedzi 3b
Sumując równania (11) i (12):
\[F_{Gz}\,=\,m_{z}a_2+m_{v}a_2\] \[F_{Gz}\,=\,\left(m_z+m_v\right)a_{2}\] \[a_2\,=\,\frac{F_{Gz}}{m_z+m_v}\]
Masa ciężarka to \(m_z\,=\,\frac{F_{Gz}}{g}\), tak więc:
\[a_2\,=\,\frac{F_{Gz}}{\frac{F_{Gz}}{g}+m_v}\tag{13}\]
Do wyrażenia (13) podstawiamy wartości liczbowe:
\[a_2\,=\,\frac{0{,}1}{\frac{0{,}1}{10}\,+\,0{,}25}\,\mathrm{m\cdot s^{-2}}\,=\, \frac{0{,}1}{0{,}26}\,\mathrm{m\cdot s^{-2}}\,=\,0{,}38\,\mathrm{m\cdot s^{-2}}\tag{14}\]
Komentarz
Wartość przyspieszenia a₁ jest większa niż przyspieszenia a₂. To dlatego, że w pierwszym przypadku siła o wartości 0,1 N działa bezpośrednio na wózek i tylko jemu nadaje przyspieszenie. W drugim przypadku siła 0,1 N, równa ciężarowi zawieszonego ciała, nadaje przyspieszenie nie tylko wózkowi, ale i samemu ciężarkowi.
PEŁNE ROZWIĄZANIE
Siły działające na wózek w przypadku a):

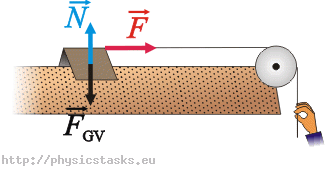
\(\vec{F}\)…siła, którą ciągnie ręka za pośrednictwem sznurka

\(\vec{N}\)…siła, z jaką strumień powietrza działa na wózek

\(\vec{F}_{Gv}\)…siła ciężaru wózka

Równanie ruchu:
\[\vec{F}_{Gv}+\vec{N}+\vec{F}\,=\, m_v\vec{a_1}\tag{1}\]
\(m_v\)…masa wózka

\(\vec{a}_1\)…przyspieszenie wózka

Aby równanie ruchu zapisać skalarnie, wprowadzamy układ odniesienia. Oś x przyjmujemy w kierunku ruchu wózka. Oś y jest prostopadła do osi x.

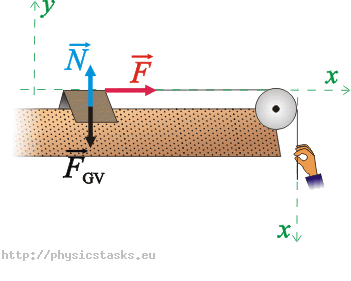
Równanie ruchu skalarnie:
\[x:\hspace{10px}F\,=\,m_{v} a_1\tag{2}\] \[y:\hspace{10px}N - F_{Gv} \,=\,0\tag{3}\]
Wózek nie porusza się wzdłuż osi y, dlatego w równaniu (3) przyrównujemy składową pionową sił do zera.

Ze związku (2) wyprowadzamy wartość przyspieszenia a₁:
\[ a_1\,=\,\frac{F}{m_v}\tag{5}\]
Podstawiamy wartości liczbowe:
\[ a_1\,=\,\frac{0{,}1}{0{,}25}\,\mathrm{m\cdot s^{-2}}\,=\, 0{,}4\,\mathrm{m\cdot s^{-2}}\tag{6}\]
Siły działające na wózek i ciężarek w przypadku b):

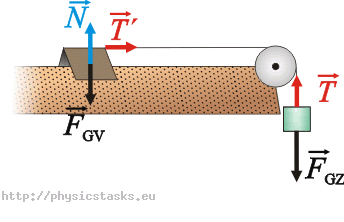
Wózek:

\(\vec{N}\)…siła działania strumienia powietrza na wózek

\(\vec{F}_{Gv}\)…siła ciężkości

\(\vec{T^{\prime}}\)…siła oddziaływania ciężarka (za pośrednictwem sznurka) na wózek

Ciężarek:

\(\vec{F}_{Gz}\)…siła ciężkości

\(\vec{T}\)…siła oddziaływania wózka (za pośrednictwem sznurka) na ciężarek

Równania ruchu:

Równanie ruchu dla wózka:
\[\vec{F}_{Gv}+\vec{N}+\vec{T^{\prime}}\,=\, m_v\vec{a}_2\tag{7}\]
Równanie ruchu dla ciężarka:
\[\vec{F}_{Gz}+\vec{T}\,=\,m_z\vec{a}_2\tag{8}\]
\(m_v\)…masa wózka

\(m_z\)…masa ciężarka

\(\vec{a}_2\)…przyspieszenie wózka i ciężarka

Aby równanie ruchu zapisać skalarnie, wprowadzamy układ odniesienia. Oś x przyjmujemy w kierunku ruchu wózka (i dalej ciężarka). Oś y jest prostopadła do osi x.

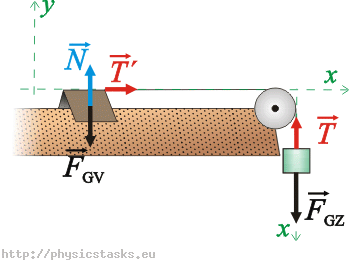
Równania ruchu skalarnie:

Równanie ruchu wózka:
\[x:\hspace{10px}T^{\prime}\,=\,m_{v}a_2\tag{9}\] \[y:\hspace{10px}N - F_{Gv}\,=\,0\tag{10}\]
Wózek nie porusza się wzdłuż osi y, dlatego w równaniu (10) przyrównujemy składową pionową sił do zera.

Równanie ruchu ciężarka:
\[x:\hspace{10px}F_{Gz}-T\,=\,m_{z}a_2\tag{11}\]
Ponieważ zaniedbujemy masę bloczka (a co za tym idzie - jego moment bezwładności), możemy w oparciu o 3. zasadę dynamiki Newtona zapisać:
\[|\vec{T}| \,=\, |\vec{T^{\prime}}|\]
Przepiszmy równanie (9):
\[T\,=\,m_{v}a_2\tag{12}\]
Dodajmy równania (11) i (12):
\[F_{Gz}\,=\,m_{z}a_2+m_{v}a_2\] \[F_{Gz}\,=\,(m_z+m_v)a_2\] \[a_2\,=\,\frac{F_{Gz}}{m_z+m_v}\]
Masa ciężarka to \[m_z\,=\,\frac{F_{Gz}}{g}\] , tak więc:
\[a_2\,=\,\frac{F_{Gz}}{\frac{F_{Gz}}{g}+m_v}\tag{13}\]
Do wzoru (13) podstawiamy wartości liczbowe:
\[a_2\,=\,\frac{0{,}1}{\frac{0{,}1}{10}\,+\,0{,}25}\,\mathrm{m\cdot s^{-2}}\,=\, \frac{0{,}1}{0{,}26}\,\mathrm{m\cdot s^{-2}}\,=\,0{,}38\,\mathrm{m\cdot s^{-2}}\tag{14}\]
PEŁNA ODPOWIEDŹ
Wartość przyspieszenia wózka, ciągniętego ręką za sznurek z siłą 0,1 N, wynosi
\[a_1\,=\,\frac{F}{m_v}\,=\,0{,}4\,\mathrm{m\cdot s^{-2}}\,.\]
Wartość przyspieszenia wózka, po zawieszeniu na sznurku ciała o ciężarze 0,1 N, wynosi
\[ a_2\,=\,\frac{F_{Gz}}{\frac{F_{Gz}}{g}+m_v}\,=\,0{,}38\,\mathrm{m\cdot s^{-2}}\,.\]
Komentarz:Wartość przyspieszenia a₁ jest większa niż przyspieszenia a₂. To dlatego, że w pierwszym przypadku siła o wartości 0,1 N działa bezpośrednio na wózek i tylko jemu nadaje przyspieszenie. W drugim przypadku siła 0,1 N, równa ciężarowi zawieszonego ciała, nadaje przyspieszenie nie tylko wózkowi, ale i samemu ciężarkowi.