Zbiór rozwiązanych zadań i problemów fizycznych

Praczłowiek i siły

Kod zadania: 891

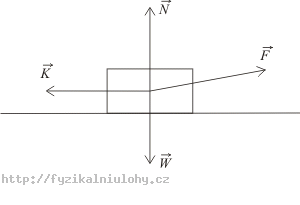
Pierwotny człowiek wciąga swoją zdobycz do jaskini działając stałą siłą \(\vec{F}\) (patrz rysunek). Ciągnie ją po chropowatej powierzchni poziomej. Wektory na rysunku przedstawiają kierunek i zwrot sił działających na zdobycz. Jaki jest związek między wartościami tych sił?

• Podpowiedź 1 - znaczenie poszczególnych sił

  Zinterpretuj znaczenie sił występujących na rysunku i opisz przyczyny ich występowania.

• Rozwiązanie do podpowiedzi 1

  Siła \(\vec{K}\) to siła tarcia pomiędzy powierzchnią zdobyczy a chropowatą powierzchnią, po której się ona porusza. Ma ona zwrot przeciwny do zwrotu wektora prędkości zdobyczy.

  Siła \(\vec{W}\) to siła ciężkości zdobyczy.

  Siła \(\vec{N}\) to siła reakcji podłoża, działająca prostopadle do powierzchni trących.

• Podpowiedź 2 - rodzaj ruchu, 1 prawo Newtona

  Jakim rodzajem ruchu porusza się ofiara? Czy można zastosować tu pierwsze prawo Newtona?

• Rozwiązanie do podpowiedzi 2

  Aby przenieść zdobycz ruchem jednostajnym, zgodnie z pierwszym prawem Newtona, wypadkowa siła działająca na ciało musi się równać zero (wektor zerowy):

  \[\vec{K}\,+\,\vec{N}\,+\,\vec{W}\,+\,\vec{F}\,=\,\vec{o}\]

• Podpowiedź 3 - rozkład sił F

  Rozkładamy siłę \(\vec{F}\) na składową poziomą (\(\vec{F}_1\)) i składową pionową (\(\vec{F}_2\)).

• Rozwiązanie do podpowiedzi 3

  Rozkład siły\(\vec{F}\) na składową poziomą \(\vec{F}_1\) i składową pionową \(\vec{F}_2\) przedstawia poniższy rysunek:

  

  Wypadkowa wszystkich sił jest równa zero, czyli wypadkowa w kierunku poziomym i wypadkowa w kierunku pionowym muszą być również równe zero:

  \[\vec{K}\,+\,\vec{F}_1\,=\,\vec{o}\] \[\vec{N}\,+\vec{W}\,+\,\,\vec{F}_2\,=\,\vec{o}\]

  Okazuje się, że:

  a) siła \(\vec{K}\) ma przeciwny zwrot niż \(\vec{F}_1\)

  b) siły \(\vec{F}_2\) i \(\vec{N}\) mają przeciwne zwroty w stosunku do wektora \(\vec{W}\)

  Możemy teraz zapisać, że:

  a) \[K\,=\,F_1\tag{1}\]

  b) \[N\,+\,F_2\,=\,W\tag{2}\]

• Podpowiedź 4

  Równanie (1) i (2) mogą być traktowane jako forma wyniku.

• Rozwiązanie do podpowiedzi 4

  Kąt między wektorami \(\vec{F}\) a \(\vec{F}_1\) oznaczamy jako α. Składowe siły \(\vec{F}\) możemy zapisać za pomocą funkcji trygonometrycznych:

  \[F_1\,=\,F\cos{\alpha}\] \[F_2\,=\,F\sin{\alpha}\]

  Równanie (1) i (2) przyjmują teraz następującą postać:

  \[K\,=\,F\cos{\alpha}\] \[N\,+\,F\sin{\alpha}\,=\,W\]

  Oczywiście \[0°\,<\,\alpha\,<\,90°,\] wartości funkcji trygonometrycznych są dodatnie i korzystamy tu z następujących nierówności:

  \[K\,<\,F\] \[N\,<\,W\]

• Rozwiązanie zadania

  Ofiara ciągnięta jest ruchem jednostajnym po poziomym torze. W tym wypadku, należy zgodnie z pierwszą zasadą dynamiki Newtona zapisać, że wypadkowa sił działających na to ciało jest równa zero (wektor zerowy), a mianowicie:

  \[\vec{K}\,+\,\vec{N}\,+\,\vec{W}\,+\,\vec{F}\,=\,\vec{o}\]

  Siłę \(\vec{F}\) możemy rozłożyć na składową poziomą \(\vec{F}_1\)  i składową pionową \(\vec{F}_2\). Ten rozkład sił przedstawiony jest na poniższym rysunku:

  

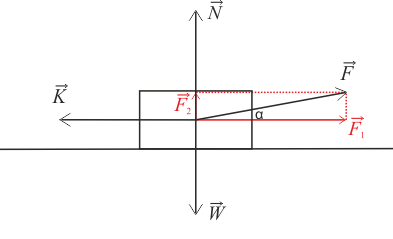
  Wypadkowa wszystkich sił jest równa 0 zarówno wzdłuż kierunku poziomego jak i pionowego:

  \[\vec{K}\,+\,\vec{F}_1\,=\,\vec{o}\] \[\vec{N}\,+\vec{W}\,+\,\,\vec{F}_2\,=\,\vec{o}\]

  Okazuje się, że:

  a) siła \(\vec{K}\) ma przeciwny zwrot niż siła\(\vec{F}_1\)

  b) siły \(\vec{F}_2\) a \(\vec{N}\) mają przeciwny zwrot niż siła \(\vec{W}\)

  Zapisujemy następujące równania:

  a) \[K\,=\,F_1\tag{1}\]

  b) \[N\,+\,F_2\,=\,W\tag{2}\]

  Pomiędzy wektorem siły \(\vec{F}\) i wektorem \(\vec{F}_1\) występuje kąt α. Składowe siły \(\vec{F}\) możemy zapisać za pomocą funkcji trygonometrycznych w następujący sposób:

  \[F_1\,=\,F\cos{\alpha}\] \[F_2\,=\,F\sin{\alpha}\]

  Równania (1) i (2) możemy zapisać teraz w następujący sposób:

  \[K\,=\,F\cos{\alpha}\] \[N\,+\,F\sin{\alpha}\,=\,W\]

  Oczywiście \(0^{\circ}\,\lt \,\alpha\,\lt \,90^{\circ}\), wartości funkcji trygonometrycznych są dodatnie i korzystamy tu z następującej nierówności:

  \[K\,\lt\,F\]

• Odpowiedź

  Spełnione są następujące nierówności:

  \[K\,\lt\,F\] \[N\,\lt\,W\]

  i poniższe równania:

  \[K\,=\,F\cos{\alpha}\] \[N\,+\,F\sin{\alpha}\,=\,W\]

  gdzie α jest kątem między wektorami \(\vec{F}\) i \(\vec{F}_1\),  \(0^{\circ}\,\lt\,\alpha\,\lt\,90^{\circ}\).