Bloczki
Kod zadania: 888
Na rysunku poniżej przedstawiono dwa krążki, blok o masie m1 i wiadro o masie m2. Oblicz wartość przyspieszenia, z którym porusza się wiadro i blok oraz wartość siły naprężenia liny T. Nie uwzględniamy masy krążków i liny. Wiadro porusza się w górę, a blok w dół.
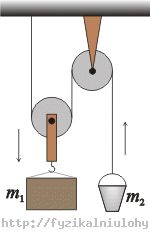
Podpowiedź 1 – działające siły i równania ruchu
Narysuj siły działające na wiadro i na blok. Napisz dwa równania ruchu dla wiadra i bloku.
Podpowiedź 2 – równania ruchu i wytrzymałość liny
Wybierz układ współrzędnych (odniesienia) i napisz równania ruchu. Zastanów się, jakie będą relacje między wektorami T, T' i T''.
Podpowiedź 3 – przyspieszenie
Zastanów się jakie są wartości przyspieszeń a1 i a2. Wyobraźmy sobie że wiadro pokonało drogę s, blok pokonał w tym czasie odległość s/2
.Podpowiedź 4 – wartości przyspieszenia, siła T
Rozwiązanie
Na rysunku poniżej przedstawiono dwa krążki, blok o masie m1 i wiadro o masie m2. Oblicz wartość przyspieszenia, z którym porusza się wiadro i blok oraz wartość siły naprężenia liny T. Nie uwzględniamy masy krążków i liny. Wiadro porusza się w górę, a blok w dół.
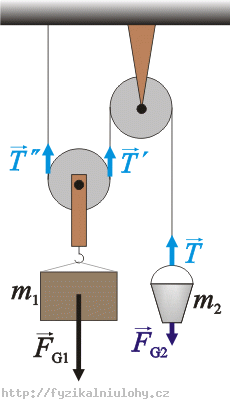
Siły działające na wiadro o masie m2:
\(\vec{F}_{G_2}\)…siła grawitacji
\(\vec{T}\)…siła, która działa na wiadro pionowo do góry
Siły działające na blok o masie m1:
\(\vec{F}_{G_1}\)…siła grawitacji
\(\vec{T^{\prime}}\)…ssiła która działa na krążek pionowo do góry
\(\vec{T^{\prime\prime}}\)…siła która działa na krążek pionowo do góry
Równanie ruchu dla wiadra:
\[\vec{F}_{G2}+\vec{T}=m_2\vec{a}_2\tag{1}\]
Równanie ruchu dla bloku:
\[\vec{F}_{G1}+\vec{T^{\prime}}+\vec{T^{\prime\prime}}=m_1\vec{a_1}\tag{2}\]
Obierzmy oś y, jak pokazano na poniższym rysunku.
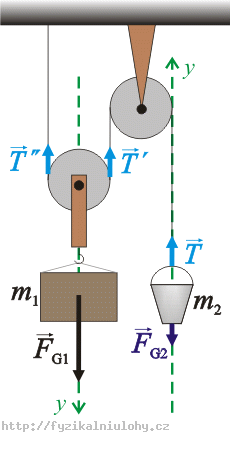
Przepiszmy równania (1) i (2) w postaci skalarnej:
\[T-F_{G2}= m_{2}a_{2}\tag{3}\]
\[F_{G1}-T^{\prime}-T^{\prime\prime} = m_{1}a_{1}\tag{4}\]
Mas krążków nie uwzględniamy, dlatego też nie mają one wpływu na naprężenie lin. Siły działające na liny mają takie same wartości:
\[|\vec{T}|=|\vec{T^{\prime}}|=|\vec{T^{\prime\prime}}|\]
Możemy przepisać równania (3) i (4):
\[T-F_{G2}= m_{2}a_{2}\tag{5}\]
\[F_{G1}-2T= m_{1}a_{1}\tag{6}\]
Związek między wartościami przyspieszeń a1 i a2 jest następujący:
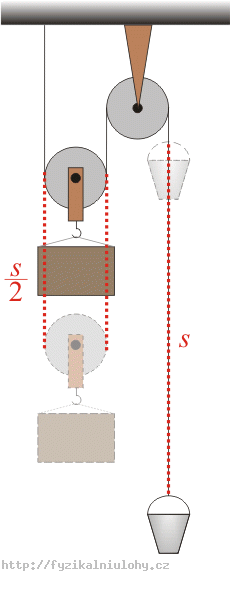
Wiadro pokonuje drogę s, natomiast blok w tym samym czasie pokonuje drogę \(\frac{s}{2}\).
\[s=\frac{1}{2}a_2t^2\]
\[\frac{s}{2}=\frac{1}{2}a_1t^2\]
Pierwsze równanie dzielimy przez drugie równanie:
\[2=\frac{a_2}{a_1}\]
\[a_2=2a_1\tag{7}\]
Równania (5) i (6) możemy teraz zapiasać następująco:
\[T-m_{2}g= m_{2}2a_1\tag{8}\]
\[m_{1}g-2T= m_{1}a_1\tag{9}\]
Otrzymujemy dwa równania (8) i (9), z dwiema niewiadomymi a1 i siłą T. Pierwsze równanie mnożymy przez 2 i równania dodajemy stronami:
\[T-m_{2}g= m_{2}2a_{1}\hspace{10px}/\cdot2\]
\[m_{1}g-2T= m_{1}a_{1}\]
Otrzymujemy:
\[m_{1}g-2m_{2}g= m_{1}a_1+4m_{2}a_1\]
\[(m_1-2m_2)g= (m_1+4m_2)a_1\]
\[a_1=\frac{(m_1-2m_2)g}{m_1+4m_2}\tag{10}\]
Zgodnie z równaniem (7) możemy zapisać:
\[a_2=2a_1=2\frac{(m_1-2m_2)g}{m_1+4m_2}=\frac{(2m_1-4m_2)g}{m_1+4m_2}\tag{11}\]Wartość siły T obliczymy korzystając ze wzoru (8):
\[T-m_{2}g= m_{2}2a_1\] \[T=m_{2}2a_1+m_{2}g=m_2\frac{2(m_1-2m_2)g}{m_1+4m_2}+m_{2}g\] \[T=\frac{2(m_{2}m_1-2m_2^2)g}{m_1+4m_2}+m_2g =\frac{(2m_{2}m_1-4m_2^2+m_2(m_1+4m_2))g}{m_1+4m_2}\] \[T=\frac{(2m_2m_1-4m_2^2+m_2m_1+4m_2^2)g}{m_1+4m_2}= \frac{3m_2m_1g}{m_1+4m_2}\] \[T=\frac{3m_2m_1g}{m_1+4m_2}\tag{12}\]Odpowiedź
Wartość przyspieszenia bloku wynosi \(a_1\,=\,\frac{(m_1-2m_2)g}{m_1+4m_2}\).
Wartość przyspieszenia wiadra wynosi \(a_2\,=\,2a_1\,=\,\frac{(2m_1-4m_2)g}{m_1+4m_2}\).
Wartość siły T naciągu liny wynosi \(T\,=\,\frac{3m_2m_1g}{m_1+4m_2}\).



