Równia pochyła - trzy ciała
Kod zadania: 885
Układ przedstawiony na rysunku zjeżdża w dół po równi pochyłej. Określ wartość przyspieszenia układu oraz sił napinających nici T1, T2. Współczynnik tarcia pomiędzy ciałami i powierzchnią równi wynosi f. Zaniedbujemy moment bezwładności bloczka i masę sznurka.
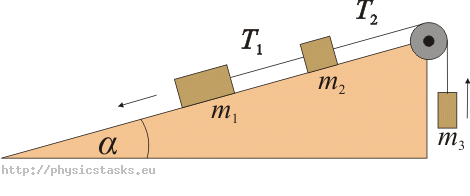
Podpowiedź 1 – równanie ruchu
Naszkicuj rysunek i zaznacz, jakie siły działają na ciało umieszczone na równi pochyłej. Zapisz odpowiednie równanie ruchu.
Podpowiedź 2 – siły tarcia
Zastanów się, od czego zależy wartość sił tarcia i jak je możemy obliczyć.
Podpowiedź 3 - wartość przyspieszenia i sił napinających nici
Uzyskaliśmy 3 równania (8), (9), (10) z trzema niewiadomymi. Po rozwiązaniu układu otrzymamy wartość przyspieszenia i sił napinających nici.
Pełne rozwiązanie
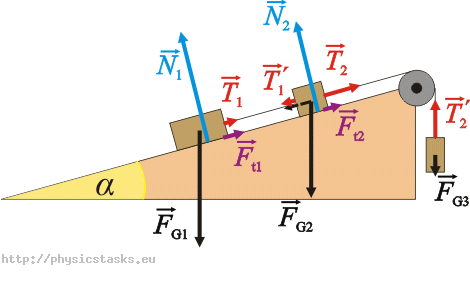
Na ilustracji zaznaczmy wszystkie siły działające na ciała i zapiszmy równania ruchu.
Siły działające na ciała:
Na pierwszą masę m1 działają siły:
\(\vec{F}_{G1}\)…ciężar ciała
\(\vec{N}_{1}\)…siła reakcji podłoża
\(\vec{T}_{1}\)…siła napinająca pierwszy sznurek
\(\vec{F}_{t1}\)…siła tarcia
Na drugą masę m2 działają siły:
\(\vec{F}_{G2}\)…ciężar ciała
\(\vec{N}_{2}\)…siła reakcji podłoża
\(\vec{T}_{2}\)…siła napinająca drugi sznurek
\(\vec{T'}_{1}\)…siła napinająca pierwszy sznurek
\(\vec{F}_{t2}\)…siła tarcia
Na trzecią masę m3 działają siły:
\(\vec{F}_{G2}\)…ciężar ciała
\(\vec{T'}_{2}\)…siła napinająca drugi sznurek
Równania ruchu dla układu:
Masy połączono sznurkami, wszystkie poruszają się z tym samym przyspieszeniem.
\[m_1:\hspace{10px}\vec{F}_{G1} + \vec{N}_{1} + \vec{F}_{t1} + \vec{T}_1\,=\,m_1\vec{a}\] \[m_2:\hspace{10px}\vec{F}_{G2} + \vec{N}_2 + \vec{F}_{t2} + \vec{T'}_1 + \vec{T}_2\,=\,m_2\vec{a}\] \[m_3:\hspace{10px}\vec{F}_{G3} + \vec{T'}_2\,=\,m_3\vec{a}\]Aby układ równań przepisać skalarnie, wprowadzamy układ współrzędnych x, y tak, by oś x miała zwrot zgodny z kierunkiem ruchu. Oś y jest prostopadła do osi x.
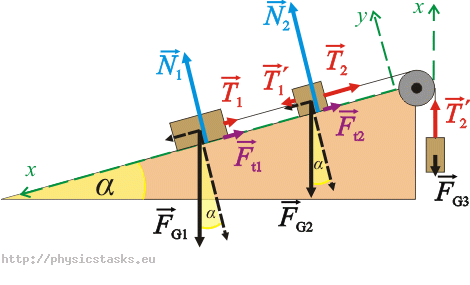
Siły \(\vec{F}_{G1}\) i \(\vec{F}_{G2}\) rozłóżmy na 2 składowe rzutując je na osie:
\[F_{G1x}\,=\,F_{G1}\sin\alpha\] \[F_{G1y}\,=\,F_{G1}\cos\alpha\] \[F_{G2x}\,=\,F_{G2}\sin\alpha\] \[F_{G2y}\,=\,F_{G2}\cos\alpha\]Równania ruchu przepiszmy skalarnie:
\[m_{x1}:\hspace{10px}F_{G1}\sin\alpha - F_{t1} - T_1\,=\,m_1a\tag{1}\] \[m_{x2}:\hspace{10px}F_{G2}\sin\alpha - F_{t2} + T'_1 - T_2\,=\,m_2a\tag{2}\] \[m_{x3}:\hspace{10px}-F_{G3} + T'_2\,=\,m_3a\tag{3}\] \[m_{y1}:\hspace{10px}N_1 - F_{G1} \cos\alpha \,=\, 0\tag{4}\] \[m_{y2}:\hspace{10px}N_2 - F_{G2} \cos\alpha \,=\, 0\tag{5}\]Nie występuje ruch wzdłuż osi y, więc dwa ostatnie równania przyrównujemy do zera.
Masa m3 działa poprzez sznurek na masę m2, a masa m2 z kolei na masę m3. Podobnie jest z masami m1 i m2. Zgodnie z 3. zasadą dynamiki Newtona siły te są równe co do wartości:
\[|\vec{T}_1| \,=\, |\vec{T'}_1|\] \[|\vec{T}_2| \,=\, |\vec{T'}_2|\]Siły tarcia:
Siła tarcia zależy od siły nacisku ciała na równię. Ta z kolei zgodnie z 3. zasadą dynamiki Newtona odpowiada sile reakcji podłoża. Zapiszmy to za pomocą równań:
\[F_{t1}\,\,=\,\,fN_1\] \[F_{t2}\,=\,fN_2\]Siły N1 i N2 wyznaczamy z równań (4) i (5):
\[N_1\,=\,F_{G1}\cos\alpha \] \[N_2\,=\,F_{G2}\cos\alpha \]Na siły tarcia otrzymamy wyrażenia:
\[F_{t1}\,=\,fF_{G1}\cos\alpha\] \[F_{t2}\,=\,fF_{G2}\cos\alpha\]Podstawmy do równań ruchu (1) i (2):
\[m_{x1}:\hspace{10px}F_{G1}\sin\alpha-fF_{G1}\cos\alpha-T_1\,=\,m_1a\tag{6}\] \[m_{x2}:\hspace{10px}F_{G2}\sin\alpha-fF_{G2}\cos\alpha+T_1-T_2\,=\,m_2a\tag{7}\]Podstawmy za \(F_{G1}\,=\,m_1g\), \(F_{G2}\,=\,m_2g\) i \(F_{G_3}\,=\,m_3g\) oraz przepiszmy równania (6), (7) i (3):
\[m_{x1}:\hspace{10px}m_1g\sin\alpha - m_1gf \cos\alpha-T_1\,=\,m_1a\tag{8}\] \[m_{x2}:\hspace{10px}m_2g\sin\alpha - m_2gf \cos\alpha + T_1 - T_2\,=\,m_2a\tag{9}\] \[m_{x3}:\hspace{10px}-m_3g + T_2\,=\,m_3a\tag{10}\]Na początek określmy wartość przyspieszenia a:
Z równań (8), (9) i (10) otrzymujemy:
\[m_1g\sin\alpha-m_1gf\cos\alpha+m_2g\sin\alpha-m_2gf\cos\alpha-m_3g\,=\,\] \[\,=\,m_2a+m_3a+m_1a\] \[a\,=\,\frac{m_1g\sin\alpha-m_1gf\cos\alpha+ m_2g\sin\alpha-m_2gf\cos\alpha-m_3g}{m_2+m_3+m_1}\] \[a\,=\,\frac{g\left[m_1(\sin\alpha-f\cos\alpha)+ m_2(\sin\alpha-f\cos\alpha)-m_3\right]}{m_2+m_3+m_1}\] \[a\,=\,\frac{(m_1+m_2)g(\sin\alpha-f\cos\alpha)-m_3g}{m_2+m_3+m_1}\tag{11}\]Teraz określmy wartość siły T1:
Podstawmy wyrażenie na przyspieszenie (11) do równania (8):
\[m_1g\sin\alpha - m_1gf \cos\alpha-T_1\,=\,\] \[\,=\,m_1\frac{(m_1+m_2)g(\sin\alpha-f\cos\alpha)-m_3g}{m_2+m_3+m_1}\]Wyznaczamy T1:
\[T_1\,=\,m_1g\sin\alpha-m_1gf \cos\alpha-m_1\frac{(m_1+m_2)g(\sin\alpha-f\cos\alpha)-m_3g}{m_2+m_3+m_1}\] \[T_1\,=\,m_1g(\sin\alpha-f\cos\alpha)-\frac{m_1g(m_1+m_2)(\sin\alpha-f\cos\alpha)-m_1m_3g}{m_2+m_3+m_1}\]Sprowadzamy do wspólnego mianownika i obliczamy:
\[T_1\,=\,\frac{m_1g(\sin\alpha-f\cos\alpha)\left[(m_2+m_3+m_1) -(m_2+m_1)\right]+m_3m_1g}{m_2+m_3+m_1}\] \[T_1\,=\,\frac{m_3m_1g\left(\sin\alpha-f\cos\alpha \right)+m_3m_1g}{m_2+m_3+m_1}\] \[T_1\,=\,\frac{m_1m_3g(1+\sin\alpha-f\cos\alpha)}{m_2+m_3+m_1}\tag{14}\]Określmy teraz wartość siły napinającej T2:
T2 wyznaczymy z równania (10):
\[T_2\,=\,m_3(a+g)\]Podstawimy wartość przyspieszenia z (11):
\[T_2\,=\,m_3\left[\frac{(m_1+m_2)g(\sin\alpha-f\cos\alpha)-m_3g} {m_2+m_3+m_1}+g \right]\]Sprowadzamy do wspólnego mianownika i obliczamy
\[T_2\,=\,m_3\left[\frac{(m_1+m_2)g(\sin\alpha-f\cos\alpha)-m_3g+(m_2+m_1)g+m_3g} {m_2+m_3+m_1}\right]\] \[T_2\,=\,\frac{m_3g(m_2+m_1)(1+\sin\alpha-f\cos\alpha)}{m_2+m_3+m_1}\tag{15}\]Odpowiedź
Wartość przyspieszenia układu wynosi
\[a\,=\,\frac{(m_1+m_2)g(\sin\alpha-f\cos\alpha)-m_3g}{m_2+m_3+m_1}\,.\]Wartość siły napinającej sznurek pomiędzy m1 i m2
\[T_1\,=\,\frac{m_1m_3g(1+\sin\alpha-f\cos\alpha)}{m_2+m_3+m_1}\,.\]Wartość siły napinającej sznurek pomiędzym2 i m3
\[T_2\,=\,\frac{m_3g(m_2+m_1)(1+\sin\alpha-f\cos\alpha)}{m_2+m_3+m_1}\,.\]




