Blok nieruchomy
Kod zadania: 887
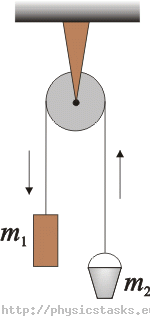
Na bloku nieruchomym wisi ciężarek o masie m1 = 0,55 kg i wiadro o masie m2 = 0,45 kg. Określ przyspieszenie układu i siłę, która działa na oś bloku. Zaniedbujemy masę bloku i sznurka oraz tarcie.
Podpowiedź 1 – równanie ruchu, określenie przyspieszenia
Naszkicuj rysunek i zaznacz na nim wszystkie siły działające na ciężarek i wiadro. Zapisz równania ruchu ciężarka i wiadra. Wprowadź układ współrzędnych.
Podpowiedź 2 – siła działająca na bloczek
Zaznacz na rysunku wszystkie siły działające na bloczek i zastanów się, jaka jest ich wypadkowa.
PEŁNE ROZWIĄZANIE
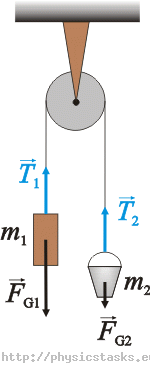
Na rysunku zaznaczmy wszystkie siły działające na wiadro i ciężarek i zapiszmy dla nich równania ruchu.
Siły działające w układzie:
Masa m1:
\(\vec{F}_{G1}\)…siła ciężkości (ciężar)
\(\vec{T_1}\)…siła napinająca sznurek
Masa m2:
\(\vec{F}_{G2}\)…siła ciężkości (ciężar)
\(\vec{T_2}\)…siła napinająca sznurek
Równania ruchu:
Masa m1:
\[\vec{F}_{G1}+\vec{T_1}\,=\,m_1\vec{a}\]Wiadro m2:
\[\vec{F}_{G2}+\vec{T_2}\,=\,m_2\vec{a}\]Ciężarek i wiadro poruszać się będą ze stałym przyspieszeniem w lewo.
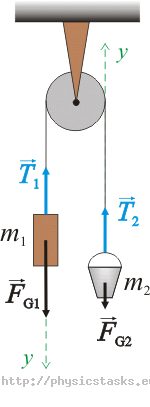
Wprowadźmy oś y, jak na rysunku. Zapiszmy równania skalarnie:
\[F_{G1} - T_1 \,=\, m_1a\tag{1}\] \[T_2 - F_{G2} \,=\, m_2a\tag{2}\]Ciężarek m1 działa poprzez sznurek na wiadro m2, a wiadro m2 z kolei na ciężarek m1. Zgodnie z 3. zasadą dynamiki Newtona siły napinające sznurek:
\[|\vec{T}_1| \,=\, |\vec{T}_2| \,=\, |\vec{T}|\,.\]Podstawiamy do równań (1) i (2):
\[m_1g - T \,=\, m_1a\tag{3}\] \[T - m_2g \,=\, m_2a\tag{4}\]Określenie przyspieszenia:
Dodając równania (3) i (4) otrzymamy:
\[m_1g - m_2g \,=\, m_1a+m_2a\] \[(m_1 - m_2)g \,=\, (m_1+m_2)a\] \[a\,=\,\frac{(m_1 - m_2)g}{m_1+m_2}\tag{5}\]Podstawmy dane liczbowe:
\[a\,=\,\left(\frac{\left(0{,}55\,-\,0{,}45\right)9{,}81}{0{,}55+0{,}45}\right)\,\mathrm{m\cdot s^{-2}}\,\dot=\,0{,}98\,\mathrm{m\cdot s^{-2}}\,.\]Określenie siły działającej na bloczek:
Na bloczek działają siły napinające sznurek \(\vec{T_1^\prime}\) i \(\vec{T_2^\prime}\) oraz równoważąca je siła \(\vec{F}_k\) (masę bloczka, a więc i jego ciężar pomijamy).
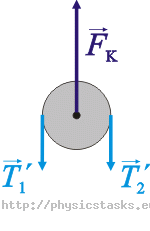
Bloczek jest nieruchomy, jego przyspieszenie wynosi zero, zachodzi więc związek:
\[\vec{T_1^\prime}\,+\,\vec{T_2^\prime}\,+\,\vec{F}_k\,=\,0\,.\tag{6}\]Zgodnie z 3. zasadą dynamiki Newtona:
\[|\vec{T_1^\prime}| \,=\, |\vec{T_2^\prime}| \,=\, |\vec{T}|\,.\]Równanie (6) przepiszmy skalarnie:
\[2T\,-\,F_k\,=\,0\] \[2T\,=\,F_k\tag{7}\]Z równań (3) lub (4) obliczamy:
\[F_k\,=\,2m_2\left(a+g\right)\,=\,2m_1\left(g-a\right)\,.\tag{8}\]Podstawiamy do równania (8) dane liczbowe:
\[F_k\,=\,2\,\cdot\,0{,}45\left(9{,}81\,+\,0{,}98\right)\,\mathrm{N}\,=\,2\,\cdot\,0{,}55\left(9{,}81\,-\,0{,}98\right)\,\mathrm{N}\] \[F_k\,=\,0{,}9\,\cdot10{,}79\,\mathrm{N}\,=\,1{,}1\,\cdot8{,}83\,\mathrm{N}\] \[F_k\,\dot{=}\,9{,}71\,\mathrm{N}\]ODPOWIEDŹ
Przyspieszenie układu wynosi \(a\,\dot{=}\,0{,}98\,\mathrm{m\cdot s^{-2}}\).
Siła działająca na bloczek \(F_k\,\dot{=}\,9{,}71\,\mathrm{N}\).




