Wycieczka rowerowa Ani
Kod zadania: 554
Ania wyjechała na wycieczkę rowerową. Na pierwszym odcinku drogi wspinała się na wzgórze w przybliżeniu ze stałą prędkością \(v_1\) – była to jedna szósta całej trasy. W kolejnym etapie podróży (jedna trzecia całej trasy) jechała na prostym odcinku drogi i podziwiała piękne krajobrazy ze stałą prędkością \(v_2\). Pozostałą część trasy pokonała w przybliżeniu ze stałą prędkością \(v_3\) .
a) Jaka jest średnia prędkość na całej trasie, którą pokonała Ania?
b) Jaka jest średnia prędkość Ani w przypadku, gdy jedną szóstą czasu zużytego na pokonanie całej trasy przejechała z prędkością \(v_1\) , jedną trzecią czasu - z prędkością \(v_2\) , a pozostały czas jechała z prędkością \(v_3\) ?
Rozwiąż to zadanie dla wartości: \(v_1 = 10 \mathrm{km/h},\,v_2 = 20\mathrm{km/h},\, v_3 = 30 \mathrm{km/h}.\)
PODPOWIEDŹ 1 a) Średnia prędkość na trasie
W jakim czasie Ania pokonała każdy odcinek swojej trasy?
Jaki był łączny czas, w którym pokonała całą trasę?
Jak w przypadku całkowitej drogi i całkowitego czasu określić średnią prędkość, z jaką jechała Ania?
Rozwiązanie
Kolejne odcinki drogi oznaczamy przez: s1, s2 i s3. Prawdą jest, że:\[s_1 = \frac{s}{6},\,\,\, s_2 = \frac{s}{3},\,\,\,s_3 = \frac{s}{2}.\]
Średnia prędkość to stosunek całkowitej drogi do całkowitego czasu, w jakim ta droga została pokonana. Drogę na każdym odcinku liczymy ze wzorów:\[s_1=v_1t_1,\,\,\,s_2=v_2t_2,\,\,\,s_3=v_3t_3.\]
Natomiast czas na każdym odcinku drogi policzymy ze wzorów:\[ t_1=\frac{s_1}{v_1} = \frac{s}{6v_1},\,\,\, t_2 = \frac{s_2}{v_2} = \frac{s}{3v_2},\,\,\, t_3 = \frac{s_3}{v_3} = \frac{s}{2v_3}.\]
Średnia prędkość jest zatem równa: \[ v_{sr} = \frac{s}{t_1 + t_2+t_3} = \frac{s}{\frac{s}{6v_1}+\frac{s}{3v_2}+\frac{s}{2v_3}} = \frac {6v_1v_2v_3}{3v_1v_2+2v_1v_3+v_2v_3}\] Po podstawieniu danych liczbowych otrzymujemy: \[ v_\mathrm{sr} =\frac{(6\cdot{10}\cdot{20}\cdot{30})\mathrm{km}}{(3\cdot{10}\cdot{20}+2\cdot{10}\cdot{30}+20{\cdot}30)\mathrm{h}} = 20 \mathrm{km/h}.\] Uwaga: Narysuj wykres prędkości w funkcji czasu (t1 = t2 = t3) oraz wykres prędkości średniej od czasu.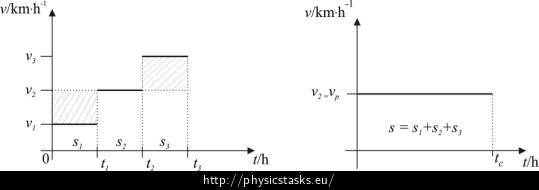
Powierzchnia pod krzywą na obu wykresach jest równa drodze pokonanej przez Anię na rowerze. Z wykresu jasno wynika, że \[ v_{sr} = v_2. \]PODPOWIEDŹ 2 b) Średnia prędkość w drugim przypadku
Należy wyrazić całkowitą drogę przebytą przez Anię. Średnią prędkość ustalamy podobnie, jak w poprzedniej części zadania.Rozwiązanie
Niech s1, s2, s3 będą odcinkami długości trasy przebytej odpowiednio z prędkościami v1, v2, v3 w czasie t1, t2, t3 oraz niech tc będzie całkowitym czasem trwania ruchu.
Z treści zadania mamy zatem:
\[t_1=\frac{t_c}{6}, t_2=\frac{t_c}{3}, t_3=\frac{t_c}{2}\]
Droga na każdym odcinku wynosi więc:
\[s_1=\frac{v_1t_c}{6}, s_2=\frac{v_2t_c}{3}, s_3=\frac{v_3t_c}{2}\]
Średnia prędkość jest obliczana w następujący sposób:
\[v_{sr}=\frac{s_1+s_2+s_3}{t_c}=\frac{\frac{v_1t_c}{6}+\frac{v_2t_c}{3}+\frac{v_3t_c}{2}}{t_c}=\frac{v_1+2v_2+3v_3}{6}\]Podstawiając dane liczbowe mamy: \[v_\mathrm{sr}=\frac{(10+2\cdot{20}+3\cdot{30})}{6} \mathrm{km/h} = 23{,}33 \mathrm{km/h} \]
Odpowiedź
Średnia prędkość to całkowita droga przebyta w całkowitym czasie, w którym następuje przemieszczenie się ciała. W pierwszym przypadku jest ona inna niż w drugim.a) \( v_\mathrm{sr} = \frac{(6\cdot{10}\cdot{20}\cdot{30})\mathrm{km}}{(3\cdot{10}\cdot{20}+2\cdot{10}\cdot{30}+20\cdot{30})\mathrm{h}} = 20 \mathrm{km/h}.\)
b) \(v_\mathrm{sr}=\frac{(10+2\cdot{20}+3\cdot{30})}{6} \mathrm{km/h} = 23{,}33 \mathrm{km/h} .\)



