Skrzynka na równi pochyłej z bloczkiem obrotowym
Kod zadania: 884
W jakim czasie skrzynka o masie m1 pokona drogę s zsuwając się po równi pochyłej o koncie nachylenia α, jeżeli jest ona połączona ze swobodnie zwisającym wiaderkiem o masie m2 poprzez linę przerzuconą przez bloczek obrotowy? Stosunek mas m1/m2 jest taki, że skrzynka porusza się w dół po równi pochyłej. Tarcie i moment bezwładność bloczka obrotowego oraz ciężar liny można zaniedbać.
Podpowiedź 1 – równania ruchu
Narysuj obrazek przedstawiający omawianą sytuację i zaznacz wszystkie siły działające na skrzynkę i wiaderko. Napisz równania ruchu dla skrzynki i wiaderka.
Podpowiedź 2 – przyspieszenie skrzynki
Z równań ruchu (4) i (5) wyznacz przyspieszenie skrzynki.
Rozwiązanie podpowiedzi 2 – przyspieszenie skrzynki
Otrzymujemy układ dwóch równań z dwoma niewiadomymi, rozwiązanie tego układu pozwala wyznaczyć przyspieszanie z jakim porusza się skrzynka.
Sumując równania (4) i (5), otrzymujemy:
\[m_1g \sin\alpha \,-\, m_2g\,=\,\left(m_1+m_2\right)a\,.\] \[a\,=\,\frac{\left(m_1 \sin\alpha \,-\, m_2\right)g}{m_1\,+\,m_2}\tag{6}\]Zależność (6) wyraża wielkość przyspieszenia z którym skrzynka zsuwa się po równi pochyłej.
Podpowiedź 3 – czas w jakim skrzynka pokonuje drogę s
Czy przyspieszenie skrzynki zależy od czasu w omawianym zadaniu? Z jakim rodzajem ruchu mamy do czynienia? Jakim wyrażeniem obliczamy drogę w ruchu, który rozpatrujemy w tym zadaniu?
KOMPLETNE ROZWIĄZANIE
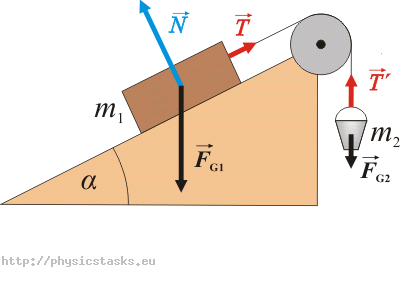
Siły działające na skrzynkę i wiaderko:
Na skrzynkę działają następujące siły:
\(\vec{F}_{G1}\)…siła ciężkości
\(\vec{N}\)…siła nacisku podłoża
\(\vec{T}\)…siła naciągu liny
Na wiaderko działają następujące siły:
\(\vec{F}_{G1}\)…siła ciężkości
\(\vec{T'}\)…siła naciągu liny
Równania ruchu:
Skrzynka i wiaderko poruszają się z takim samym przyspieszeniem.
Dla skrzynki:
\[\vec{F}_{G1}+\vec{N}+\vec{T}\,=\,m_1\vec{a}\]Dla wiaderka:
\[\vec{F}_{G2}+\vec{T'}\,=\,m_2\vec{a}\]Przepisujemy równania w formie skalarnej, w tym celu definiujemy układ współrzędnych x, y tak, że oś x jest równoległa do kierunku ruchu skrzynki (wiaderka), natomiast oś y jest prostopadła do osi x.
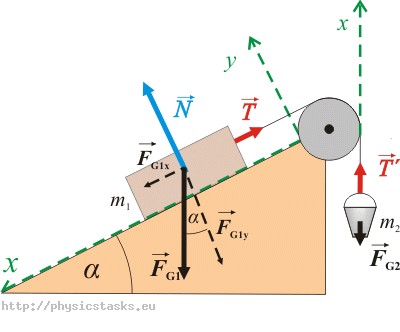
Siłę \(F_{G1}\) rozkładamy na składowe prostopadłe wzdłuż osi.
\[F_{G1x}\,=\,F_{G1}\sin\alpha\] \[F_{G1y}\,=\,F_{G1}\cos\alpha\]Równania ruchu przepisujemy w formie skalarnej:
Dla skrzynki:
\[x:\hspace{10px}F_{G1} \sin\alpha - T \,=\, m_1a\tag{1}\] \[y:\hspace{10px}N - F_{G1} \cos\alpha \,=\, 0\tag{2}\]Skrzynka nie porusza się w kierunku osi y wobec czego składowa przyspieszenia w tym kierunku jest równa zeru.
Dla wiaderka:
\[x:\hspace{10px}T' - F_{G2} \,=\, m_2a\tag{3}\]Ponieważ zaniedbujemy ciężar bloczka obrotowego, możemy również pominąć wpływ jego momentu bezwładności na naciąg liny. Wobec czego wiaderko oddziałuje bezpośrednio poprzez linę na skrzynkę i odwrotnie skrzynka oddziałuje bezpośrednio na wiaderko. Zgodnie z trzecim prawem Newtona:
\[\left|\vec{T}\right|\,=\,\left|\vec{T'}\right|.\]Podstawiając za \(F_{G1}\,=\,m_1g\), \( F_{G2}\,=\,m_2g\) przepisujemy równania (1) i (3) w postaci:
\[m_1g \sin\alpha - T \,=\, m_1a\tag{4}\] \[T - m_2g\,=\, m_2a\tag{5}\]Otrzymujemy układ dwóch równań z dwoma niewiadomymi, rozwiązanie tego układu pozwala wyznaczyć przyspieszanie z jakim porusza się skrzynka.
Sumując równania (4) i (5), otrzymujemy:
\[m_1g \sin\alpha \,-\, m_2g\,=\,\left(m_1+m_2\right)a\,.\] \[a\,=\,\frac{\left(m_1 \sin\alpha \,-\, m_2\right)g}{m_1\,+\,m_2}\tag{6}\]Zależność (6) wyraża wielkość przyspieszenia z którym skrzynka zsuwa się po równi pochyłej.
Wyznaczenie czasu w jakim skrzynka przebywa drogę s:
Z równania (6) widzimy, że przyspieszenie jest niezależne od czasu, mówimy wówczas o ruchu jednostajnie przyspieszonym, dla takiego ruchu wzór na drogę s ma następującą postać:
\[s\,=\,\frac{at^2}{2}\,.\tag{7}\]t… czas, w którym skrzynka pokona drogę s
Z wyrażenia (7) wyznaczamy czas t:
\[t\,=\, \sqrt{\frac{2s}{a}}\,.\tag{8}\]Do równania (8) wstawiamy wyrażenie na przyspieszenie z równania (6):
\[t\,=\,\sqrt{\frac{2s\left(m_1\,+\,m_2\right)}{\left(m_1 \sin\alpha \,-\, m_2\right)g}}\,.\tag{9}\]ODPOWIEDŹ KOŃCOWA
Skrzynka pokona drogę s na równi pochyłej w czasie \[t\,=\,\sqrt{\frac{2s\left(m_1\,+\,m_2\right)}{\left(m_1 \sin\alpha \,-\, m_2\right)g}}\] .



