Ciężarówka na stoku
Kod zadania: 890
Ciężarówka jedzie z góry ze stałą prędkością 30 km·h−1. Masa samochodu wynosi 5 t. Samochód hamuje silnikiem, całkowita siła hamowania ma wartość 4400 N. Wyznacz kąt nachylenia stoku góry.
Zapis danych
m = 5 t masa samochodu Fb = 4400 N siła hamowania v = 30 km·h−1 prędkość samochodu α = ? (°) kąt nachylenia stoku Podpowiedź 1
Jakie siły działają na samochód? Jaki jest ich kierunek i zwrot? Sporządź pomocniczy rysunek.
Podpowiedź 2
Co możemy powiedzieć na temat wymienionych sił w myśl 1. zasady dynamiki Newtona?
Podpowiedź 3
Rozłóż siłę ciężkości \(\vec{F}_G\) na składowe równoległą i prostopadłą do podłoża. Jakie warunki spełniać powinny te składowe w myśl 1. zasady dynamiki Newtona?
Podpowiedź 4
Spróbuj wyrazić składową F0 za pomocą siły ciężkości. Wykorzystaj związki trygonometryczne oraz daną wartość siły Fb do określenia z równania (4) kąta α.
Pełne rozwiązanie
Na samochód działają trzy siły:
1) Siła ciężkości \(\vec{F}_G\) skierowana pionowo w dół.
2) Siła reakcji podłoża \(\vec{R}\) (samochód naciska na podłoże, więc w myśl 3. zasady dynamiki Newtona podłoże działa na samochód). Ta siła skierowana jest prostopadle do podłoża.
3) Siła hamowania \(\vec{F}_b\), skierowana wzdłuż stoku, przeciwnie do kierunku ruchu.
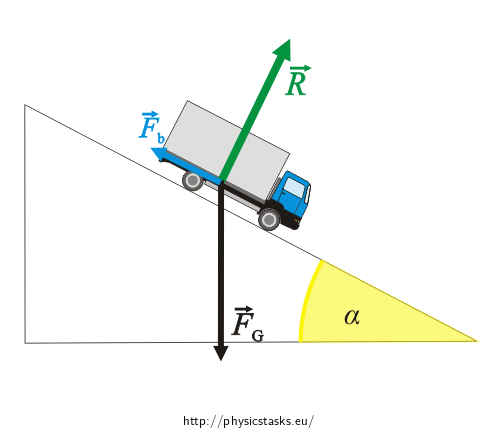
Ponieważ samochód porusza się ruchem jednostajnym prostoliniowym, siła wypadkowa (suma tych trzech sił) musi wynosić zero (wektor zerowy):
\[\vec{F}_G \,+\,\vec{R}\,+\,\vec{F}_b\,=\,\vec{o}\]Siłę ciężkości \(\vec{F}_G\) możemy rozłożyć na składowe \(\vec{F}_0\) równoległą do stoku i \(\vec{F}_n\) prostopadłą do podłoża. Rozkład ten pokazuje kolejny rysunek:
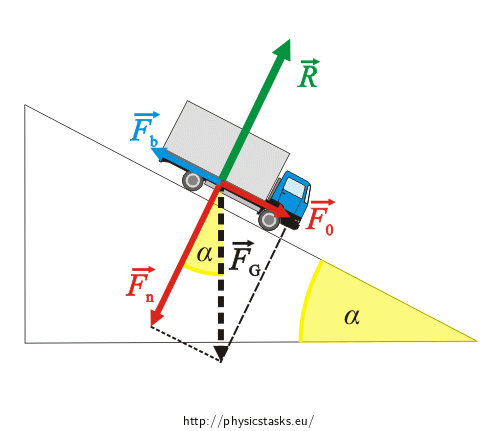
Z 1. zasady dynamiki Newtona wynika, że sumy poszczególnych składowych - równoległych i prostopadłych do kierunku ruchu - muszą się zerować. Spełnione więc będą warunki:
\[\vec{F}_n\,+\,\vec{R}\,=\,\vec{o}\tag{1}\] \[\vec{F}_0\,+\,\vec{F}_b\,=\,\vec{o}\tag{2}\]Ponieważ siły \(\vec{F}_n\) i \(\vec{R}\) oraz \(\vec{F}_0\) i \(\vec{F}_b\) mają przeciwny zwrot, możemy zapisać równania na wartości tych sił:
\[F_n\,-\,R\,=\,0\tag{3}\] \[F_0\,-\,F_b\,=\,0\tag{4}\]Do dalszych obliczeń wykorzystamy równanie (4).
Z trygonometrii (patrz rysunek wyżej):
\[\sin{\alpha}\,=\,\frac{F_0}{F_G}\]Zatem:
\[F_0\,=\,F_G\sin{\alpha}\tag{5}\]Siłę ciężkości FG wyrażamy za pomocą masy samochodu m:
\[F_G\,=\,mg\,,\tag{6}\]gdzie g to przyspieszenie grawitacyjne. Podstawiając (6) do (5) otrzymamy:
\[F_0\,=\,mg\sin{\alpha}\tag{7}\]Korzystając z (4) i (7) zapisujemy:
\[ mg\sin{\alpha}\,-\,F_b\,=\,0\,\Rightarrow\,\sin{\alpha}\,=\,\frac{F_b}{mg}\]
Podstawiając dane liczbowe:
\[F_b\,=\,4400\,\mathrm{N}\] \[m\,=\,5\,\mathrm{t}\,=\,5000\,\mathrm{kg}\] \[g\,=\,9{,}81\,\mathrm{m{\cdot}s^{-2}}\] \[\sin{\alpha}\,=\,\frac{F_b}{mg}\,=\,\left(\frac{4400}{5000{\cdot}9{,}81}\right)\,\dot{=}\,0{,}090\,\Rightarrow\,\alpha\,\dot{=}\,5^\circ8^{\prime}\]Warto zauważyć, że kąt nachylenia nie zależy od prędkości samochodu, ale od siły hamowania.
Odpowiedź
\[\sin{\alpha}\,=\,\frac{F_b}{mg}\,=\,0{,}090\,\Rightarrow\,\alpha\,=\,5^{\circ} 8^{\prime}\]Stok nachylony jest pod kątem ok. \(5^{\circ} 8^{\prime}\).


