Klocek na równi pochyłej
Kod zadania: 886
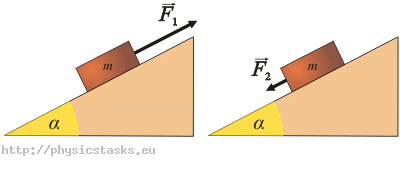
Klocek możemy przesuwać po równi ruchem jednostajnym z dołu do góry używając siły F1, zaś z góry na dół - używając siły F2. Wyznacz współczynnik tarcia f klocka o równię, jeśli F1 = 6F2, a obie siły są równoległe do powierzchni równi, która z kolei tworzy z poziomem kąt α = 15°.
Podpowiedź 1 – siły działające na klocek na równi pochyłej
Naszkicuj rysunek i zaznacz na nim wszystkie siły działające na klocek:
1) Klocek przesuwamy siłą F1 w górę.
2) Klocek przesuwamy siłą F2 w dół.
Zapisz równanie ruchu dla każdego z tych przypadków.
Podpowiedź 2 – siła tarcia, określenie współczynnika tarcia
Zastanów się, od czego zależy siła tarcia i jak możemy ją obliczyć. Podstaw wyrażenie na siłę tarcia do równań ruchu (1) i (3). Otrzymasz 2 równania z dwiema niewiadomymi. Określ z nich współczynnik tarcia.
PEŁNE ROZWIĄZANIE
Na rysunku zaznaczymy wszystkie siły działające na klocek w obu przypadkach i napiszemy równania ruchu.
Siły działające na klocek:
Na klocek w obu przypadkach działają następujące siły:
\(\vec{F}_{G}\)…siła ciężkości (ciężar)
\(\vec{F}_1(\vec{F}_2)\)…siła, którą ciągniemy klocek
\(\vec{N}\)…siła reakcji podłoża
\(\vec{F}_{t}\)…siła tarcia
Kierunki i zwroty sił zaznaczono na rysunku.
Ruch w górę:
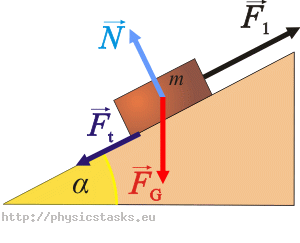
Ruch w dół:
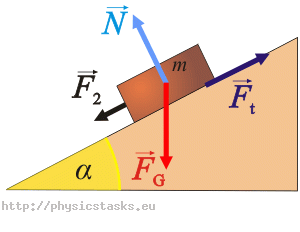
Równania ruchu:
Ruch w górę:
\[\vec{F}_G+\vec{N}+\vec{F}_1+\vec{F}_t\,=\,m\vec{a}_1\,=\,0\,.\]Ruch w dół:
\[\vec{F}_G+\vec{N}+\vec{F}_2+\vec{F}_t\,=\,m\vec{a}_2\,=\,0\,.\]Obydwa ruchy są jednostajne, przyspieszenie w każdym przypadku wynosi zero.
Równania ruchu skalarnie:
Wprowadźmy układ współrzędnych tak, aby oś x była skierowana wzdłuż równi. Oś y jest prostopadła do osi x.
Siłę \[F_G\] rozłóżmy na 2 składowe:
\[F_{Gx}\,=\,F_G\sin\alpha\] \[F_{Gy}\,=\,F_G\cos\alpha\]Ruch w górę:
\[x:\hspace{10px}-F_G\sin\alpha+F_1-F_t\,=\,0\tag{1}\] \[y:\hspace{10px}N-F_G\cos\alpha\,=\,0\tag{2}\]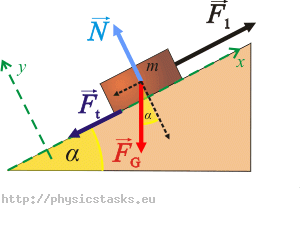
Ruch w dół:
\[x:\hspace{10px}F_G\sin\alpha+F_2-F_t\,=\,0\tag{3}\] \[y:\hspace{10px}N-F_G\cos\alpha\,=\,0\tag{4}\]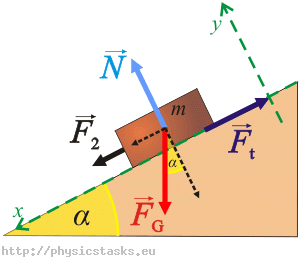
Siła tarcia:
Siła tarcia klocka o równię zależy od siły nacisku. Ta z kolei zgodnie z 3. zasadą dynamiki Newtona odpowiada sile reakcji podłoża. Zapiszmy to za pomocą równań:
\[F_t\,=\,fN\,.\]Siłę N wyznaczymy z równania (2):
\[N\,=\,F_G\cos\alpha\,. \]Na siłę tarcia mamy wyrażenie:
\[F_t\,=\,fF_G\cos\alpha\,.\]Obliczenie współczynnika tarcia:
Podstawmy do równań ruchu (1) i (3) wyrażenie na siłę tarcia. Siłę F1 zapiszmy jako 6F2.
\[-F_G\sin\alpha+6F_2-F_Gf\cos\alpha\,=\,0\tag{6}\] \[F_G\sin\alpha+F_2-F_Gf\cos\alpha\,=\,0 \hspace{10px}\tag{7}\]Równanie (7) mnożymy obustronnie przez 6 i odejmujemy od niego równanie (6):
\[-F_G\sin\alpha+6F_2-F_Gf\cos\alpha\,=\,0\] \[6F_G\sin\alpha+6F_2-6F_Gf\cos\alpha\,=\,0\]
\[7F_G\sin\alpha-5F_Gf\cos\alpha\,=\,0\] \[7F_G\sin\alpha\,=\,5F_Gf\cos\alpha\hspace{20px}|:(5F_G\cos\alpha)\] \[f\,=\,\frac{7}{5}\mathrm{tg}\alpha\tag{8}\]Podstawiamy do wzoru (8) dane liczbowe:
\[f\,=\,\frac{7}{5}\,\mathrm{tg}15°\,\dot{=}\,\frac{7}{5}\cdot0{,}268\,\dot{=}\,0{,}38\]PEŁNA ODPOWIEDŹ
Współczynnik tarcia między klockiem a równią wynosi \(f=\frac{7}{5}\mathrm{tg}\alpha\,\dot{=}\,0{,}38\).



