Rescue Plane
Task number: 1992
A rescue plane flies to help a drowning man. The pilot keeps the plane at a constant height of 1200 m above the water surface and heads directly above the man’s head (see the diagram). The speed of the plane is 430 km·h−1.
At what angle of view must the pilot release the rescue bag in order to let it fall as close to the man as possible?
Neglect the resistance of environment.
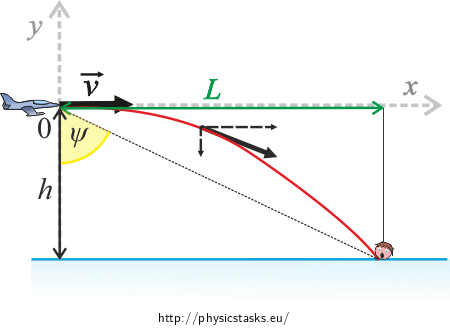
Given values
h = 1200 m height of the plane above the water surface v = 430 km·h−1 speed of the plane ψ = ? (°) angle of view From the tables: g = 9.81 m·s−2 gravitational acceleration Hint 1: Initial velocity of the bag
What is the initial velocity of the bag? Do you know its magnitude?
Hint 2: Duration of the fall on the surface
What is the motion of the bag in a vertical direction?
How can you determine the time t it takes before the bag hits the water surface if you know at what height h above the surface it was released?
Hint 3: Distance L
What is the motion of the bag in a horizontal direction?
What horizontal distance L will the bag travel in time t, that is the duration of its fall to the surface? You know the duration of the fall t from the previous hint.
Hint 4: View angle ψ
How can you determine the angle of view ψ at which the pilot must release the rescue bag in order to let it fall as close to the man as possible?
Look at the diagram. What trigonometric function will you use in your calculation?
What quantities do you need to express the angle of view ψ? Do you know them?
OVERALL SOLUTION
The initial velocity of the bag is identical to the velocity of the plane. Therefore it has the magnitude v.
If we neglect the resistance of environment, the bag moves vertically in a free fall.
Because we know at what height it was released, we can easily determine the duration of its fall to the surface. It holds in the direction of the y axis that:
\[-h\,=\,-\,\frac{1}{2}gt^{2}\,,\]therefore:
\[h\,=\,\frac{1}{2}gt^{2}\,.\](only the gravitational force acts upon the bag in the direction of the y axis)
By solving this equation we obtain for the duration of the flight t:
\[t\,=\,\sqrt{\frac{2h}{g}}\,.\]The bag (and the plane) move horizontally with constant speed v.
From the previous hint we see that for the duration of the fall to the surface t holds:
\[t\,=\,\sqrt{\frac{2h}{g}}\,.\]In this time, the bag travels the horizontal distance:
\[L\,=\,vt\,.\]By substituting for t we obtain:
\[L\,=\,v\,\sqrt{\frac{2h}{g}}\,.\]The way to calculate the angle of view ψ is obvious from the diagram.
We will use the trigonometric function tangens.
In our calculation, we need to know the distance L the bag will travel horizontally during the time t before it hits the surface and the height from which it falls. We know both.
It holds that:
\[\mathrm{tg}\psi\,=\,\frac{L}{h}\,=\,\frac{v\,\sqrt{\frac{2h}{g}}}{h}\,=\,v\,\sqrt{\frac{2}{hg}}\,.\]Numerically:
\[\mathrm{tg}\psi\,=\frac{430\, 000}{3\, 600}\sqrt{\frac{2}{1\, 200{\cdot}9.81}}\,\dot=\, 1.556\,,\] \[\psi\,=\,57^{\circ}\,.\]Note: the horizontal projection of the velocity of the bag is at every moment identical with the velocity of the plane, so the pilot always sees the falling bag directly below him.
Answer
The pilot must release the bag under the angle of view ψ, for which it holds that:
\[\mathrm{tg}\psi\,=\,v\,\sqrt{\frac{2}{hg}}\,\dot=\,1.556\,,\] \[\psi\,=\,57^{\circ}\,.\]





