Rolling of a Ball

Task number: 1993

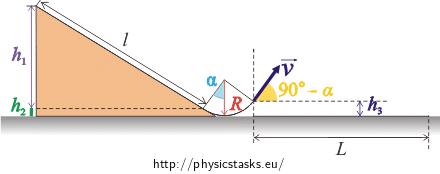
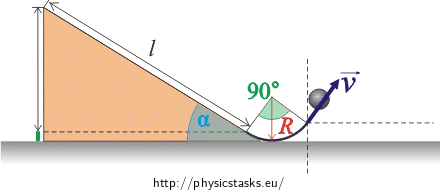
A small ball rolls down an inclined plane with lenght l = 2 m which makes an angle α = 30° with the horizontal plane. The inclined plane ends with an arc with radius R = 0.4 m and central angle of 90° (see the diagram).

The speed at which the ball leaves the end of the arc is v = 3.5 m·s⁻¹ .

a) Determine the maximum height H above the horizontal plane to which the ball will get after leaving the path.

b) Determine the time T during which the ball is in the air after leaving the path.

c) Determine the horizontal distance L from the point where it will leave the path to the point it will hit the ground.

Given values

l = 2 m	length of the inclined plane
α = 30°	angle the inclined plane makes with the horizontal plane
R = 0.4 m	radius of the arc
v = 3.5 m·s⁻¹	speed at which the ball leaves the end of the arc
H = ? (m)	maximum height reached by the ball
T = ? (s)	time during which the ball is in the air
L = ? (m)	distance at which the ball lands
From the tables
g = 9.81 m·s⁻²	acceleration of gravity

Hint 1: Free body diagram
How can you describe the movement of the ball after it leaves the path?

Draw a free body diagram and mark into it all the quantities needed for your calculations.

Write all the necessary relations between the quantities derived from the diagram.
Solution of Hint 1
The ball is launched from initial height h₃ at an elevation angle of 90°−α with initial velocity \(\vec{v}\) (see Fig.1).

Fig.1:

Fig.2:

A few relations can be derived from diagrams 1 and 2 for angle α and the given values:
\[h_1\,=\,l\sin\alpha\,,\] \[h_2\,=\,R\left(1\,-\,\cos\alpha\right)\,,\] \[h_3\,=\,R\left[1\,-\,\cos(90^{\circ}-\alpha)\right]\,=\,R\left(1\,-\,\sin\alpha\right)\,,\] \[H\,=\,h_3\,+\,h_4\,.\]
Hint 2 for a): Maximum height
What relations (for coordinates and components of velocity) hold for a projectile launched at elevation angle 90°−α with initial speed v?

How do you express the maximum height the ball reaches after leaving the path using these relations?
Solution of Hint 2
For a projectile launched at elevation angle 90°−α with initial speed v we then obtain:
\[v_\mathrm{x}\,=\,v\,\cos(90^{\circ}-\alpha)\,=\,v\,\sin\alpha\,,\] \[v_\mathrm{y}=v\sin(90^{\circ}-\alpha)-gt=v\cos\alpha-gt\,,\] \[x\,=\,vt\,\sin\alpha\,,\] \[y\,=\,vt\,\cos\alpha\,-\,\frac{1}{2}gt^{2}\,.\]
For maximum height:
\[v_\mathrm{y}\,=\,0\,,\] \[t_\mathrm{v}\,=\,\frac{v\,\cos\alpha}{g}\,,\] \[h_4\,=\, vt_\mathrm{v}\,\cos\alpha\,-\,\frac{1}{2}gt_\mathrm{v}^{2} \,=\, \frac{v^{2}\,\cos^{2}\alpha}{g}\,-\,\frac{gv^{2}\,\cos^{2}\alpha}{2g^{2}}\,=\,\frac{v^{2}\,\cos^{2}\alpha}{2g}\,,\] \[H \,=\, h_3 \,+\, h_4 \,=\, R\,\left(1\,-\,\sin\alpha\right)\,+\,\frac{v^{2}\,\cos^{2}\alpha}{2g}\,.\]
Numerically:
\[H\,=\,\left[0.4\,\left(1\,-\,\frac{1}{2}\right)\,+\,\frac{3.5^{2}\cdot \left(\frac{\sqrt{3}}{2}\right)^{2}}{2{\cdot} 9.81}\right]\,\mathrm{m}\,,\] \[H\,\dot=\,0.67\,\mathrm{m}\,.\]
Hint 3 for b): Duration of the flight
The time in which the ball is in the air consists of the time it rises and the time it falls.

How can you calculate these times?
Solution of Hint 3
Duration of rising:
\[t_\mathrm{v}\,=\,T_1\,=\,\frac{v\,\cos\alpha}{g}\,.\]
Duration of falling (the ball is falling from height H):
\[H\,=\,\frac{1}{2}gT_2^{2}\,,\] \[T_2\,=\,\sqrt{\frac{2H}{g}}\,.\]
Total duration of the flight:
\[T\,=\,T_1\,+\,T_2\,=\,\frac{v\,\cos\alpha}{g}\,+\,\sqrt{\frac{2H}{g}}\,.\]
Numerically:
\[T\,=\,\left[\frac{3.5\cdot\frac{\sqrt{3}}{2}}{9.81}\,+\,\sqrt{\frac{2{\cdot} 0.67}{9.81}}\right]\,\mathrm{s}\,,\] \[T\,\dot=\,0.68\,\mathrm{s}\,.\]
Hint 4 for c): Distance of the flight
Denote the horizontal distance from the point the ball leaves the arc as L and mark it into the diagram.

How can you calculate it?
Solution of Hint 4
The horizontal movement of the ball is uniformly linear with speed v sinα for duration T.

The horizontal distance L from the point the ball leaves the arc is then:
\[L\,=\,vT\,\sin\alpha\,.\]
Numerically:
\[L=\left(3.5{\cdot} 0.68\cdot \frac{1}{2}\right)\,\mathrm{m}\,,\] \[L\,\dot=\,1.19\,\mathrm{m}\,.\]
OVERALL SOLUTION:
a) Maximum height

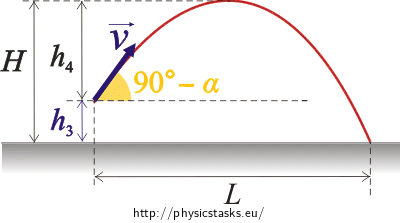
The ball is launched from initial height h₃ at an elevation angle of 90° − α with initial velocity \(\vec{v}\) (see Fig.1).

Fig.1:

Fig.2:

A few relations can be derived from diagrams 1 and 2 for angle α and the given values:
\[h_1\,=\,l\sin\alpha\,,\] \[h_2\,=\,R\left(1\,-\,\cos\alpha\right)\,,\] \[h_3\,=\,R\left[1\,-\,\cos(90^{\circ}-\alpha)\right]\,=\,R\left(1\,-\,\sin\alpha\right)\,,\] \[H\,=\,h_3\,+\,h_4\,.\]
For a projectile launched at elevation angle 90°−α with initial speed v we then obtain:
\[v_\mathrm{x}\,=\,v\,\cos(90^{\circ}-\alpha)\,=\,v\,\sin\alpha\,,\] \[v_\mathrm{y}=v\sin(90^{\circ}-\alpha)-gt=v\cos\alpha-gt\,,\] \[x\,=\,vt\,\sin\alpha\,,\] \[y\,=\,vt\,\cos\alpha\,-\,\frac{1}{2}gt^{2}\,.\]
For maximum height:
\[v_\mathrm{y}\,=\,0\,,\] \[t_\mathrm{v}\,=\,\frac{v\,\cos\alpha}{g}\,,\] \[h_4\,=\, vt_\mathrm{v}\,\cos\alpha\,-\,\frac{1}{2}gt_\mathrm{v}^{2} \,=\, \frac{v^{2}\,\cos^{2}\alpha}{g}\,-\,\frac{gv^{2}\,\cos^{2}\alpha}{2g^{2}}\,=\,\frac{v^{2}\,\cos^{2}\alpha}{2g}\,,\] \[H \,=\, h_3 \,+\, h_4 \,=\, R\,\left(1\,-\,\sin\alpha\right)\,+\,\frac{v^{2}\,\cos^{2}\alpha}{2g}\,.\]
Numerically:
\[H\,=\,\left[0.4\,\left(1\,-\,\frac{1}{2}\right)\,+\,\frac{3.5^{2}\cdot \left(\frac{\sqrt{3}}{2}\right)^{2}}{2{\cdot} 9.81}\right]\,\mathrm{m}\,,\] \[H\,\dot=\,0.67\,\mathrm{m}\,.\]
b) Flight duration

Duration of rising:
\[t_\mathrm{v}\,=\,T_1\,=\,\frac{v\,\cos\alpha}{g}\,.\]
Duration of falling (the ball is falling from height H):
\[H\,=\,\frac{1}{2}gT_2^{2}\,,\] \[T_2\,=\,\sqrt{\frac{2H}{g}}\,.\]
Total duration of the flight:
\[T\,=\,T_1\,+\,T_2\,=\,\frac{v\,\cos\alpha}{g}\,+\,\sqrt{\frac{2H}{g}}\,.\]
Numerically:
\[T\,=\,\left[\frac{3.5\cdot\frac{\sqrt{3}}{2}}{9.81}\,+\,\sqrt{\frac{2{\cdot} 0.67}{9.81}}\right]\,\mathrm{s}\,,\] \[T\,\dot=\,0.68\,\mathrm{s}\,.\]
c) Flight distance

The horizontal movement of the ball is uniformly linear with speed v sinα for duration T.

The horizontal distance L from the point the ball leaves the arc is then:
\[L\,=\,vT\,\sin\alpha\,.\]
Numerically:
\[L=\left(3.5{\cdot} 0.68\cdot \frac{1}{2}\right)\,\mathrm{m}\,,\] \[L\,\dot=\,1.19\,\mathrm{m}\,.\]
Answer
a) For the maximum height above the horizontal plane the ball reaches after leaving the path it holds that:
\[H\,=\,R\left(1\,-\,\sin\alpha\right)\,+\,\frac{v^{2}\,\cos^{2}\alpha}{2g}\,\dot=\,0.67\,\mathrm{m}\,.\]
b) The time the ball spends in the air after leaving the path is:
\[T\,=\,T_1\,+\,T_2\,=\,\frac{v\,\cos\alpha}{g}\,+\,\sqrt{\frac{2H}{g}}\,\dot=\,0.68\,\mathrm{s}\,.\]
c) The horizontal distance from the point the ball leaves the arc is:
\[L\,=\,vT\,\sin\alpha\,\dot=\,1.19\,\mathrm{m}\,.\]