Basketball player
Task number: 926
A basketball hoop is placed at a height h1 above the floor. The centre of the basket is at a distance L horizontally from the free-throw line. A basketball player shoots free throws and the ball leaves his hand in a moment where its centre is exactly above the free-throw line at a height h2 above the floor.
The optimal elevation angle α is an angle in which the centre of the ball passes through the hoop centre, while the minimal initial ball velocity is needed. Prove generally, that this angle is α = 45˚+β/2, where β is the tangent angle, i.e. the deviation of a line connecting the hoop centre and the starting point of the shot from the horizontal plane.
Determine the optimal elevation angle for given values and calculate the corresponding initial velocity of the ball.
Air resistance is negligible.
Solve for values h1 = 3.05 m, L = 5.425 m, h2 = 2.45 m, g = 9.81 m·s-2 .
Given values
h1 = 3.05 m height of basket hoop above the floor L = 5.425 m horizontal distance between hoop centre and the free-throw line h2 = 2.45 m height of ball centre above the floor when ball centre is placed directly above the free-throw line α = ? optimal elevation angle v0 = ? (m·s−1) initial velocity of the ball corresponding to optimal elevation angle From the Handbook of Chemistry and Physics: g = 9.81 m·s−2 acceleration of gravity Hint 1: Sketch of the situation
Draw a picture depicting the situation, mark the elevation and tangent angles, the distance L and the height of the basket hoop above the place, from which we throw the ball.
Hint 2: Motion of the ball in horizontal and vertical direction
What kind of motion is carried out by the ball in horizontal direction? What kind of motion is carried out by the ball in vertical direction?
Hint 3: Velocity of the ball in horizontal and vertical direction
What is the velocity of the ball in horizontal direction and how does the x-coordinate of the ball change with time?
What is the velocity of the ball in vertical direction and how does the y-coordinate of the ball change with time?
What values do the x and y coordinates reach when the ball flies into the basket hoop? Write down the equations needed and evaluate the square of the initial velocity v02 (use the relationship \(\mathrm{tg}\beta = \frac{H}{L}\)).
Hint 4: Minimum value of velocity
For what angle α bis the value of v02 minimal?
Hint 5: Initial velocity for optimum angle
Calculate the initial velocity v0 for the optimum angle α that is, for the case where \[ \mathrm{sin}(2α-β) = 1.\] Express the sine and cosine of the angle β using the distances H and L.
Overall solution:
Let us denote L and H the horizontal and vertical distance of the hoop from the starting point of the throw, let the elevation angle be α, β the tangent angle, t is the time of the ball flight, v0 is the initial velocity of the ball and v is the velocity of the ball passing through the hoop (see Figures 1, 2)
Figure 1:
\[H = h_1 - h_2\]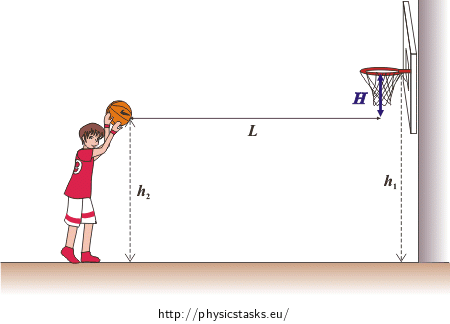
Figure 2:
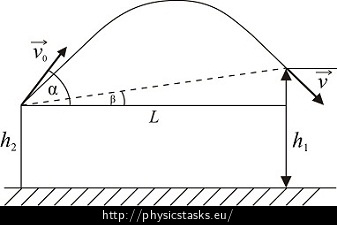
In the horizontal direction the ball performs a uniform rectilinear motion. The motion in the vertical direction is a vertical throw upwards.
The following applies:
\[v_x=v_0\cos\alpha,\] \[v_y=v_0\sin\alpha-gt,\] \[x=v_0t\cos\alpha,\] \[y=v_0t\sin\alpha-\frac{1}{2}gt^{2}.\]At the moment the ball flies into the basket hoop it applies:
\[x=L=v_0t\cos\alpha.\]Thus:
\[t=\frac{L}{v_0\cos\alpha},\] \[y=H=v_0t\sin\alpha-\frac{1}{2}gt^{2}=L\mathrm{tg}\alpha-\frac{gL^{2}}{2v_0^{2}\cos^{2}\alpha}.\]From here:
\[\frac{gL^{2}}{2v_0^{2}\cos^{2}\alpha} = L\mathrm{tg}\alpha- H,\] \[\frac{gL^{2}}{L\mathrm{tg}\alpha- H} = 2v_0^{2}\cos^{2}\alpha,\] \[v_0^{2}=\frac{gL^{2}}{2(L\mathrm{tg}\alpha-H)\cos^{2}\alpha}=\frac{gL^{2}}{2(L\sin\alpha\cos\alpha-H\mathrm{cos^{2}}\alpha)}.\]After substituting \[H=L\mathrm{tg}\beta\] and adjusting we obtain
\[v_0^{2}=\frac{gL^{2}}{2(L\sin\alpha\cos\alpha-L\mathrm{tg}\beta\cos^{2}\alpha)}=\frac{gL}{\mathrm{sin}2\alpha-\mathrm{tg}\beta(1+\cos2\alpha)},\] \[v_0^{2}=\frac{gL\cos\beta}{\sin2\alpha\cos\beta-\sin\beta-\sin\beta\cos2\alpha}=\frac{gL\cos\beta}{\sin(2\alpha-\beta)-\sin\beta}.\]Note: When adjusting, we used the following trigonometric relationships:
\[2\sin\alpha\cos\alpha = \sin2\alpha,\] \[\cos2\alpha =\mathrm{cos}^{2}\alpha - sin^{2}\alpha,\] \[\sin(2\alpha-\beta) = \mathrm{sin}2\alpha\cos\beta - \mathrm{cos}2\alpha\sin\beta.\]The value of the expression is minimal, if value of the denominator is maximal, namely if:
\[\sin(2\alpha-\beta)=1,\] \[2\alpha-\beta=90^{\circ}.\]That is when the following applies:
\[\alpha=45^{\circ}+\frac{\beta}{2}.\]In such a case:
\[v_0^{2}=\frac{gL\cos\beta}{1-\sin\beta}.\]The following applies:
\[\cos\beta = \frac{L}{\sqrt{H^{2}+L^{2}}}, \] \[\sin\beta = \frac{H}{\sqrt{H^{2}+L^{2}}}, \]using ; \[H = h_1 - h_2,\]
\[\cos\beta = \frac{L}{\sqrt{(h_1 - h_2)^{2}+L^{2}}}, \] \[\sin\beta = \frac{h_1 - h_2}{\sqrt{(h_1 - h_2)^{2}+L^{2}}}.\]Then:
\[v_0^{2}=\frac{\frac{gL^{2}}{\sqrt{H^{2}+L^{2}}}}{1-\frac{H}{\sqrt{H^{2}+L^{2}}}}=\frac{gL^{2}}{\sqrt{H^{2}+L^{2}}-H}=g\left(\sqrt{H^{2}+L^{2}}+H\right),\]using \[H = h_1 - h_2,\]
\[v_0^{2}=g\left(\sqrt{(h_1 - h_2)^{2}+L^{2}}+(h_1 - h_2)\right).\]Numerical solution for given values
\[\sin\beta = \frac{3.05-2.45}{\sqrt{(3.05 - 2.45)^{2}+5.425^{2}}},\] of which: \[\beta\,\dot{=}\,6^{\circ}.\] Then: \[\alpha=45^{\circ}+\frac{\beta}{2},\] \[\alpha\,\dot{=}\,48^{\circ}.\] Furthermore: \[v_0^{2}=9.81\left(\sqrt{(3.05 - 2.45)^{2}+5.425^{2}}+(3.05 - 2.45)\right)\,\mathrm{m^{2}.s^{-2}},\] \[v_0\,\dot{=}\,7.7\,\mathrm{m.s^{-1}}.\]Answer
The optimum elevation angle is
\[\alpha=45^{\circ}+\frac{\beta}{2},\] where \[\sin\beta = \frac{h_1 - h_2}{\sqrt{(h_1 - h_2)^{2}+L^{2}}}. \]
For given values:
\[\alpha\,\dot{=}\,48^{\circ}.\]The corresponding size of the initial velocity of the ball is:
\[v_0^{2}=g\left(\sqrt{(h_1 - h_2)^{2}+L^{2}}+(h_1 - h_2)\right).\]For given values:
\[v_0\,\dot{=}\,7.7\,\mathrm{m.s^{-1}}.\]




