A garden hose

Task number: 506

We want to splash as high as possible on a vertical wall (which is situated at a horizontal distance d from the hose’s nozzle) with a jet of water flowing from a garden hose with an initial speed v₀.

a) What elevation angle α do we need to choose?

b) At what height h does the water splash on the wall?

c) At what angle ψ does the water hit the wall? Determine the angle (from the horizontal) of the instantaneous velocity vector at the moment of the hit.

Disregard the air resistance.

Solve for these values: v₀= 15 m·s^-1, d = 10 m.

Analysis
We want to determine the elevation angle α at which we have to aim the hose so that the water splashes as high as possible. First we have to express how the height of the splash h depends on the angle α. Then we can find the maximum of the function h(α).

Beware of the idea that the maximum height of the splash on the wall will correspond to the maximum height of the throw for a given angle α. Realize that the distance to the wall is fixed. Draw the different possible situations.
Hint 1 for a): picture of the situation, type of motion
Draw a picture of the situation. What kind of motion is it? How do the x-component and y-component of the speed of the water change with time? How do the x-component and y-component of the coordinates change?
Solution to Hint 1 for a): picture of the situation, type of motion

We choose the origin of the coordinate system at the garden hose’s nozzle.

It is an inclined throw, in other words projectile motion.

The x-component and y-component of the speed of the water and the x-component and y-component of the coordinates change with time in the following way:
\[v_x=v_0\cos\alpha\tag{1}\] \[v_y=v_0\sin\alpha-gt\tag{2}\]

\[x=v_0t\cos\alpha\tag{3}\] \[y=v_0t\sin\alpha-\frac{1}{2}gt^{2}\tag{4}\]
Hint 2 for a): time of flight of the water to the wall, height h of the range
How long does it take the water to reach the wall for a fixed angle α? What height h of the water splash on the wall corresponds to this time?
Solution to Hint 2 for a): time of flight of the water to the wall, height h of the range
The time of flight of the water and the height of the splash on the wall follow these relations:
\[x=d\]
Then we get from (3):
\[d=v_0t\cos\alpha\] \[t=\frac{d}{v_0\cos\alpha}\tag{5}\]

\[y=h\]
Then we get from (4):
\[h=v_0t\sin\alpha-\frac{1}{2}gt^{2}\]
We substitute for t from (5):
\[h=dtg\alpha-\frac{gd^{2}}{2v_0^{2}\cos^{2}\alpha}=dtg\alpha-\frac{gd^{2}}{2v_0^{2}}(1+tg^{2}\alpha)\tag{6}\]
Hint 3 for a): the elevation angle α
We need to find out for what angle α is the height h of the splash on the wall maximal. We want to find the maximum of the function h = h(α). How can we do it?
Solution to Hint 3 for a): the elevation angle α
We find when the derivative of the function h with respect to α equals zero:
\[\frac{dh}{d\alpha}=\frac{d}{d\alpha}(dtg\alpha-\frac{gd^{2}}{2v_0^{2}\cos^{2}\alpha})\] \[\frac{dh}{d\alpha}=\frac{d}{\cos^{2}\alpha}-\frac{gd^{2}\sin\alpha}{v_0^{2}\cos^{3}\alpha}=\frac{d}{\cos^{2}\alpha}\left(1-\frac{gd}{v_0^{2}}tg\alpha\right)=0\] \[1-\frac{gd}{v_0^{2}}tg\alpha = 0\] \[tg\alpha=\frac{v_0^{2}}{gd}\tag{7}\]

The function h(α) reaches its maximum for elevation angle \(\alpha=arctg\frac{v_0^{2}}{gd} \).

For the given values:
\[tg\alpha=\frac{15^{2}}{9.81{\cdot}10} = 2.294\] \[\alpha=arctg2{,}294=66.4^{\circ}\]
Hint 4 for b): the maximum height of the water splash
You know the angle for the maximum height of the splash and also the dependence of the height h of the splash on the wall on the angle α. You can find the maximum height easily.
Solution to Hint 4 for b): the maximum height of the water splash
You know that the height of the splash on the wall is according to equation (6):
\[h=dtg\alpha-\frac{gd^{2}}{2v_0^{2}\cos^{2}\alpha}=dtg\alpha-\frac{gd^{2}}{2v_0^{2}}(1+tg^{2}\alpha)\tag{6}\]

You know that the height h of the splash on the wall will be maximal for the angle α which according to equation (7) is:
\[tg\alpha=\frac{v_0^{2}}{gd}\tag{7}\]

We substitute from equation (7) into equation (6):
\[h=\frac{dv_0^{2}}{gd}-\frac{gd^{2}}{2v_0^{2}}\left(1+\frac{v_0^{4}}{g^{2}d^{2}}\right)=\frac{v_0^{2}}{2g}-\frac{gd^{2}}{2v_0^{2}}\]

Numerically:
\[h=(\frac{15^{2}}{2{\cdot}9.81}-\frac{9.81{\cdot}10^{2}}{2{\cdot}15^{2}})\,\mathrm{m}\] \[h=9.29\,\mathrm{m}\]
Hint 5 for c): deviation ψ at which the water hits the wall
We draw in the picture the vector of the velocity of the water at the moment it hits the wall and its components in the direction of the x-axis and y-axis. Using that we can easily express the appropriate angle. We determine both components of the speed at the moment of the hit by equations (1) and (2) from Hint 1.
Solution to Hint 5 for c): deviation ψ at which the water hits the wall

We determine the angular deviation ψ from the horizontal direction of the final velocity from the equation:
\[tg\psi=\frac{v_y}{v_x}\]
We substitute for v_x and v_y from equations (1) and (2) and for the time t from equation (5):
\[tg\psi=\frac{v_0\sin\alpha-gt}{v_0\cos\alpha}=tg\alpha-\frac{gd}{v_0^{2}\cos^{2}\alpha}\]
We adjust using equation (7):
\[tg\psi=tg\alpha-\frac{1}{tg\alpha\cos^{2}\alpha}\] \[tg\psi=tg\alpha-\frac{1}{\sin\alpha\cos\alpha}=\frac{\sin^{2}\alpha-1}{\sin\alpha\cos\alpha}=-\frac{1}{tg\alpha}= -\frac{gd}{v_0^{2}}\]

Numerically:
\[tg\psi=-\frac{9.81{\cdot}10}{15^{2}} = -0.436\] \[\psi=-23.6^{\circ}\]
The deviation ψ of the final velocity of the water from the horizontal direction is negative (we subtract the magnitude in the clockwise direction). See the picture.

Note:

Beware of the idea that at the maximum height of the splash on the wall y-component of the speed will be zero and thus the deviation ψ will be zero too. In the task the distance to the wall is fixed and thus, for the given angle, the time of flight of the water is also fixed.
COMPLETE SOLUTION:

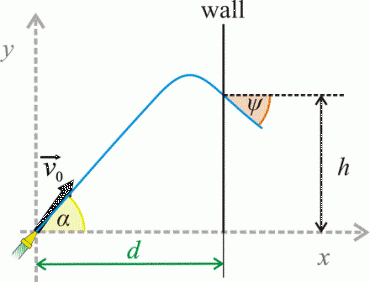
a) The elevation angle

We choose the origin of the coordinate system at the garden hose’s nozzle.

It is an inclined throw, in other words projectile motion.

The x-component and y-componentof the speed of the water and the x-component and y-component of the coordinates change with time in the following way:
\[v_x=v_0\cos\alpha\tag{1}\] \[v_y=v_0\sin\alpha-gt\tag{2}\]

\[x=v_0t\cos\alpha\tag{3}\] \[y=v_0t\sin\alpha-\frac{1}{2}gt^{2}\tag{4}\]
The time of flight of the water and the height of the splash on the wall follow these relations:
\[x=d\]
Then we get from (3):
\[d=v_0t\cos\alpha\] \[t=\frac{d}{v_0\cos\alpha}\tag{5}\]

\[y=h\]
Then we get from (4):
\[h=v_0t\sin\alpha-\frac{1}{2}gt^{2}\]
We substitute for t from (5):
\[h=dtg\alpha-\frac{gd^{2}}{2v_0^{2}\cos^{2}\alpha}=dtg\alpha-\frac{gd^{2}}{2v_0^{2}}(1+tg^{2}\alpha)\tag{6}\]
We need to find out for what angle α is the height h of the splash on the wall maximal. We want to find the maximum of the function h = h(α).

We find when the derivative of the function h with respect to α equals zero:
\[\frac{dh}{d\alpha}=\frac{d}{d\alpha}(dtg\alpha-\frac{gd^{2}}{2v_0^{2}\cos^{2}\alpha})\] \[\frac{dh}{d\alpha}=\frac{d}{\cos^{2}\alpha}-\frac{gd^{2}\sin\alpha}{v_0^{2}\cos^{3}\alpha}=\frac{d}{\cos^{2}\alpha}\left(1-\frac{gd}{v_0^{2}}tg\alpha\right)=0\] \[1-\frac{gd}{v_0^{2}}tg\alpha = 0\] \[tg\alpha=\frac{v_0^{2}}{gd}\tag{7}\]

The function h(α) reaches its maximum for elevation angle \(\alpha=arctg\frac{v_0^{2}}{gd}\).

For the given values:
\[tg\alpha=\frac{15^{2}}{9.81{\cdot}10} = 2.294\] \[\alpha=arctg2.294=66.4^{\circ}\]

b) The maximum height of the water splash

You know that the height of the splash on the wall is according to equation (6):
\[h=dtg\alpha-\frac{gd^{2}}{2v_0^{2}\cos^{2}\alpha}=dtg\alpha-\frac{gd^{2}}{2v_0^{2}}(1+tg^{2}\alpha)\tag{6}\]

You know that the height h of the splash on the wall will be maximal for the angle α which according to equation (7) is:
\[tg\alpha=\frac{v_0^{2}}{gd}\tag{7}\]

We substitute from equation (7) into equation (6):
\[h=\frac{dv_0^{2}}{gd}-\frac{gd^{2}}{2v_0^{2}}\left(1+\frac{v_0^{4}}{g^{2}d^{2}}\right)=\frac{v_0^{2}}{2g}-\frac{gd^{2}}{2v_0^{2}}\]

Numerically:
\[h=(\frac{15^{2}}{2{\cdot}9.81}-\frac{9.81{\cdot}10^{2}}{2{\cdot}15^{2}})\,\mathrm{m}\] \[h=9.29\,\mathrm{m}\]

c) The deviation ψ of the velocity vector of the splashing water from the horizontal direction

We mark in the picture the velocity vector of the splashing water, its components and the desired angle.

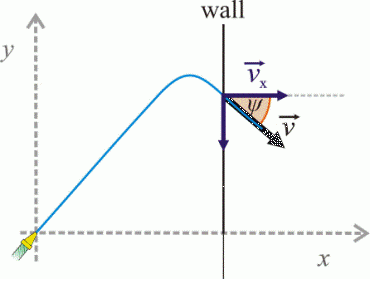
We determine the angular deviation ψ from the horizontal direction of the final velocity from the equation:
\[tg\psi=\frac{v_y}{v_x}\]
We substitute for v_x and v_y from equations (1) and (2) and for the time t from equation (5):
\[tg\psi=\frac{v_0\sin\alpha-gt}{v_0\cos\alpha}=tg\alpha-\frac{gd}{v_0^{2}\cos^{2}\alpha}\]
We adjust using equation (7):
\[tg\psi=tg\alpha-\frac{1}{tg\alpha\cos^{2}\alpha}\] \[tg\psi=tg\alpha-\frac{1}{\sin\alpha\cos\alpha}=\frac{\sin^{2}\alpha-1}{\sin\alpha\cos\alpha}=-\frac{1}{tg\alpha}= -\frac{gd}{v_0^{2}}\]

Numerically:
\[tg\psi=-\frac{9.81{\cdot}10}{15^{2}} = -0.436\] \[\psi=-23.6^{\circ}\]
The deviation ψ of the final velocity of the water from the horizontal direction is negative (we subtract the magnitude in the clockwise direction). See the picture.

Note:

Beware of the idea that at the maximum height of the splash on the wall the y- component of the speed will be zero and thus the deviation ψ will be zero too. In the task the distance to the wall is fixed and thus, for the given angle, the time of flight of the water is also fixed.
Answer
a) If we want to splash the water at the maximum height on the vertical wall, we have to choose the elevation angle α for which:
\[\alpha=arctg\frac{v_0^{2}}{gd}\]

For the given values:
\[\alpha=66.4^{\circ}\]

b) The water splashes to the height h, for which this formula holds:
\[h=\frac{v_0^{2}}{2g}-\frac{gd^{2}}{2v_0^{2}}\]

For the given values:
\[h=9.29\,\mathrm{m}\]

c) The water hits the wall at the deviation ψ given by:
\[tg\psi=-\frac{gd}{v_0^{2}}\]

For the given values:
\[\psi=-23.6^{\circ}\]