Annie's Ride
Task number: 1995
Annie went for a bike ride. At first, she was going up a hill with approximately constant speed of 10 km·h−1. Like that she drove one sixth of the overall route. The next part of her ride equaled one third of the overall route and was straight, but because she rode through a beautiful countryside which she wanted to enjoy, she accelerated but a little and was now moving with a speed of 20 km·h−1. The rest of the trip she was hurrying home, so she drove with a constant speed of 30 km·h−1.
a) What was her average speed on the overall route?
b) How great would her average speed be in case she moved for a third of the way with a speed of 10 km·h−1, one third with a speed of 20 km·h−1 and the rest of the way with speed of 30 km·h−1?
Analysis
v1 = 10 km·h−1 Annie’s speed in the first part v2 = 20 km·h−1 Annie’s speed in the second part v3 = 30 km·h−1 Annie’s speed in the third part vp = ? (km·h−1) Annie’s average speed Hint 1 for a): Average speed on the overall route
Express each of the times Annie needed to make the parts of the route. How long did it take her to travel the whole route? How do you find average velocity with overall time and overall distance?
Hint 2 for b): verage speed in case b)
Again, express the lengths of each of the parts of the route using velocity and time. Then express the overall distance traveled. Now you can easily find the average speed as you did in the previous part.
COMPLETE SOLUTION
ad a)
We mark the overall route s, its parts s1, s2, s3.
We know that:
\[s_1\,=\,\frac{s}{6} \,,\hspace{30px} s_2\,=\,\frac{s}{3} \,,\hspace{30px} s_3\,=\,\frac{s}{2}\,.\]It also holds that:
\[s_1\,=\,v_1t_1 \,,\hspace{30px} s_2\,=\,v_2t_2 \,,\hspace{30px} s_3\,=\,v_3t_3\,.\]So:
\[t_1 \,=\, \frac{s_1}{v_1} \,=\, \frac{s}{6v_1} \,,\hspace{30px} t_2\,=\,\frac{s_2}{v_2} \,=\, \frac{s}{3v_2} \,,\hspace{30px} t_3\,=\,\frac{s_3}{v_3} \,=\, \frac{s}{2v_3}\,.\]We find the average velocity as distance traveled over time of travel:
\[v_p\,=\,\frac{s}{t_1+t_2+t_3}\,=\,\frac{s}{\frac{s}{6v_1}+\frac{s}{3v_2}+\frac{s}{2v_3}}\,=\,\frac{6v_1v_2v_3}{3v_1v_2+2v_1v_3+v_2v_3}\,.\]Numerically:
\[v_p\,=\,\frac{(6{\cdot} 10\cdot 20{\cdot} 30)\,\mathrm{km}}{(3{\cdot} 10\cdot 20+2{\cdot} 10\cdot 30+20{\cdot} 30)\,\mathrm{h}}\,=\,20\,\mathrm{km\cdot h^{-1}}\,.\]Note:
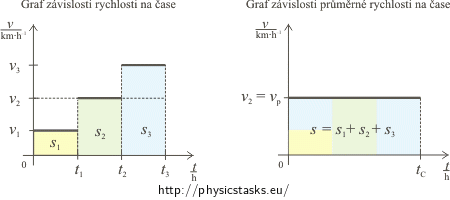
We can solve this problem graphically, too. We draw a graph of speed dependence on time (t1 = t2 = t3) and a graph of average speed dependence on time.
Area under the curve in both graphs represents the distance traveled and must equal. From graphs it is obvious that vp = v2.
ad b)
We mark the parts of Annie’s route s1, s2, s3 the speeds with which she traveled v1, v2, v3 and times t1, t2, t3, the overall time tc.
We know that:
\[t_1\,=\,\frac{t_c}{6}\,,\hspace{30px}t_2\,=\,\frac{t_c}{3}\,,\hspace{30px}t_3\,=\,\frac{t_c}{2}\,.\]For the parts of the route it holds that:
\[s_1\,=\,\frac{v_1t_c}{6}\,,\hspace{30px}s_2\,=\,\frac{v_2t_c}{3}\,,\hspace{30px}s_3\,=\,\frac{v_3t_c}{2}\,.\]This is how we calculate the average speed vp :
\[v_p\,=\,\frac{s_1+s_2+s_3}{t_c}\,=\,\frac{\frac{v_1t_c}{6}+\frac{v_2t_c}{3}+\frac{v_3t_c}{2}}{t_c}\,=\,\frac{v_1+2v_2+3v_3}{6}\,.\]Numerically:
\[v_p\,=\,\frac{(10+2{\cdot} 20+3{\cdot} 30)}{6}\,\mathrm{km\cdot h^{-1}}\dot=23{,}3\,\mathrm{km\cdot h^{-1}}\,.\]Answer
a) Annie’s average speed on the overall route is:
\[v_p=\frac{6v_1v_2v_3}{3v_1v_2+2v_1v_3+v_2v_3}\,.\]Numerically:
\[v_p\,=\,20\,\mathrm{km\cdot h^{-1}}\,.\]b) In case Annie was moving with a speed v1 for a sixth of time she traveled, third of the time with a speed v2 and the rest of overall time with a speed of v3, her average speed is:
\[v_p = \frac{v_1+2v_2+3v_3}{6}\,.\]Numerically:
\[v_p\,\dot=\,23{,}3\,\mathrm{km\cdot h^{-1}}\,.\]