A girl pulls a sledge on some snowy pavement

Task number: 380

A girl pulls a loaded sledge with mass m = 20 kg on some horizontal snowy pavement. The velocity of the sledge is constant. The coefficient of kinetic friction μ_k between the runner and the pavement is 0.1 and the angle φ between the cord and the pavement is 30°. Find:

1) The acceleration of the sledge

2) The magnitude of the tension force by which the girl affects the sledge

3) The magnitude of the normal force by which the sledge affects the pavement

4) The magnitude of the friction force that affects the sledge

Hint 1 – Acceleration of the sledge, the force that affects the sledge
What does it mean for the acceleration (and also the resulting force) when the velocity is constant? Draw a picture and mark all the forces that affect the sledge. Use Newton’s second law \((\Sigma\vec{F} = m\vec{a}) \) and write the vector motion equation for the sledge.
Solution of Hint 1 – Acceleration of the sledge, the force that affects the sledge
Acceleration of the sledge:

If the velocity of the sledge is constant, its velocity doesn’t change with time and thus the acceleration of the sledge equals zero \((\vec{a} = 0)\).

Forces that affect the sledge:

\(\vec{F}_{G}\)…the weight

\(\vec{N}\)…force by which the pavement affects the sledge vertically (the normal force)

\(\vec{T}\)…desired tension force by which the girl pulls the sledge

\(\vec{F}_{t}\)…friction force which opposes the sledge’s motion

The vector motion equation for the sledge:

(since \( \vec{F}_{net} = m \vec{a} \), and \(\vec{a} = 0 \), the vector sum of the forces must be zero)
\[ \vec{F}_{G}+ \vec{N} + \vec{T} + \vec{F}_{t} = m\vec{a} = 0 \tag{1}\]
Hint 2 – The scalar motion equations
The motion equations need to be written down in scalar form. Choose the appropriate coordinate system, find the components of the forces in the corresponding directions and rewrite the motion equations in these directions.
Solution of Hint 2 – The scalar motion equations
Choose the x-axis horizontally in the direction of the motion and choose the y-axis vertically.

The force equation in the x-direction:
\[ \sum^\ F_x = T\cos\varphi - F_{t} = 0 \tag{2}\]
The force equation in the y-direction:
\[ \sum^\ F_y = N + T\sin\varphi - F_G = 0 \tag{3}\]
Note: We usually choose one of the axes in the direction of the motion and the other axis perpendicularly to the direction of the motion.
Hint 3 – The magnitudes of the tension force and the friction force
Think about what the friction force depends on and how it could be expressed.
Solution of Hint 3 – The magnitudes of the tension force and the friction force
The friction force is directly proportional to the force by which the sledge affects the pavement. This force is, according to Newton’s third law, of the same magnitude as the force by which the pavement affects the sledge.

The friction force F_t can be expressed as:

\[F_t =\mu_k N\tag{4}\]

The force N (by which the pavement affects the sledge vertically) can be expressed using equation (3):

\[N = mg - T\sin\varphi\tag{5}\]

Equations (4) and (5) give:

\[F_{t} = \mu_{k}(mg - T\sin\varphi)\tag{6}\]

Substitute equation (6) into equation (2):

\[T\cos\varphi - \mu_{k}(mg - T\sin\varphi) = 0\]

\[T\cos\varphi - \mu_k mg + \mu_k T\sin\varphi = 0\]

\[T(\cos\varphi + \mu_k\sin\varphi)-\mu_k mg= 0\tag{7}\]

From equation (7) express the tension force:
\[T = \frac{mg\mu_{k}}{\cos\varphi + \mu_{k}\sin\varphi}\tag{8}\]
Hint 4 – The magnitude of the normal force
The force by which the sledge affects the pavement is according to Newton’s third law of the same magnitude as the force by which the pavement affects the sledge. The magnitude of the force N (by which the pavement affects the sledge) is given by equation (5): \[N = mg - T\sin\varphi\tag{5}\] It just remains to substitute.
Solution of Hint 4 – The magnitude of the normal force
The force N (by which the pavement affects the sledge) is given by equation (5):
\[N = mg - T\sin\varphi\tag{5}\]
Substitute for T from equation (8), yielding the expression:
\[N = mg - \frac{mg\mu_{k}}{\cos\varphi + \mu_{k}\sin\varphi}\sin\varphi = mg (1 - \frac{\mu_{k}\sin\varphi}{\cos\varphi + \mu_{k}\sin\varphi})=\] \[\,\,\,\,\,\,\,\,= mg(\frac{\cos\varphi}{\cos\varphi + \mu_{k}\sin\varphi}) = mg(\frac{1}{1 + \mu_{k}\tan\varphi})\tag{9}\]
Hint 5 – The magnitude of the friction force
The magnitude of the friction force F_t is given by equation (4): \[F_{t} = \mu_{k} N \tag{4}\] It just remains to substitute.
Solution of Hint 5 – The magnitude of the friction force
The magnitude of the friction force F_t is given by equation (4):
\[F_{t} = \mu_{k} N \tag{4}\]
If you substitute for N in equation (4) using equation (9), then:
\[F_{t} = mg(\frac{1}{1 + \mu_{k}\tan\varphi})\mu_{k}\tag{10}\]
Note: The friction force F_t isn’t generally equal to the product mgμ_k, because the cord „lifts“ the sledge, therefore it affects the pavement less and the perpendicular normal force N is less than mg.
COMPLETE SOLUTION OF POINT 1 – Acceleration of the sledge
If the velocity of the sledge is constant, its velocity doesn’t change with time and thus the acceleration of the sledge equals zero \((\vec{a} = 0).\)

Answer: The acceleration of the sledge a equals zero.
COMPLETE SOLUTION OF POINT 2 – The magnitude of the tension force
Forces that affect the sledge:

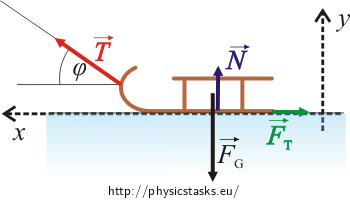
\(\vec{F}_{G} \)...the weight

\(\vec{N} \)...force by which the pavement affects the sledge vertically (the normal force)

\(\vec{T}\)...desired tension force by which the girl pulls the sledge

\(\vec{F}_{t}\)...friction force which opposes the sledge’s motion

The vector motion equation for the sledge:

(since \( \vec{F}_{net} = m \vec{a} \), and \(\vec{a} = 0 \), the vector sum of the forces must be zero)

\[\vec{F}_{G}+\vec{N}+\vec{T}+\vec{F}_{t}=m\vec{a}=0\tag{1}\]

m…mass of the sledge

\(\vec{a}\)…acceleration of the sledge

Because the velocity \(\vec{v}\) is constant, the acceleration \(\vec{a}\) equals zero and the resultant force that affects the sledge is also equal to zero.

Choose the appropriate coordinate system and rewrite the motion equations in scalar form. Choose the x-axis horizontally in the direction of the motion and choose the y-axis vertically – as shown in the picture.

The force equation in the x-direction:
\[ \sum^\ F_x = T\cos\varphi - F_{t} = 0 \tag{2}\]
The force equation in the y-direction:
\[ \sum^\ F_y = N + T\sin\varphi - F_G = 0 \tag{3}\]
The friction force is directly proportional to the force by which the sledge affects the pavement. This force is according to Newton’s third law of the same magnitude as the force by which the pavement affects the sledge.

The friction force F_t can be expressed as:

\[F_t = \mu_k N \tag{4}\]

The force N (by which the pavement affects the sledge) can be expressed using equation (3):

\[N = mg - T\sin\varphi\tag{5}\]

Equations (4) and (5) give:

\[F_{t} = \mu_{k}(mg - T\sin\varphi)\tag{6}\]

Substitute equation (6) into equation (2), and then write the projection to the x-axis as:
\[T\cos\varphi - \mu_{k}(mg - T\sin\varphi) = 0\tag{7}\]
Express the tension force from the equation (7):
\[T = \frac{mg\mu_{k}}{\cos\varphi + \mu_{k}\sin\varphi}\tag{8}\]
For the given numerical values we get from (8):
\[T = \frac{20{\cdot}9.81{\cdot}0.1}{\cos 30^{\circ} + 0.1\cdot\sin30^{\circ}}\,\textrm{N} =\frac{19.62}{\frac{\sqrt{2}}{2} + 0.1{\cdot}0.5}\,\textrm{N}\] \[T=21.4\,\textrm{N}\]
Answer: The magnitude of the tension force T by which the girl pulls the sledge is 21.4 N.
COMPLETE SOLUTION OF POINT 3 – The magnitude of the normal force
The force by which the sledge affects the pavement is according to Newton’s third law of the same magnitude as the force by which the pavement affects the sledge. The magnitude of the force N (by which the pavement affects the sledge) is given by equation (5):
\[N = mg - T\sin\varphi\tag{5}\]
Substitute for T from equation (8), and you get the expression:
\[N = mg - \frac{mg\mu_{k}}{\cos\varphi + \mu_{k}\sin\varphi}\sin\varphi = mg (1 - \frac{\mu_{k}\sin\varphi}{\cos\varphi + \mu_{k}\sin\varphi})=\] \[\,\,\,\,\,\,\,\,= mg(\frac{\cos\varphi}{\cos\varphi + \mu_{k}\sin\varphi}) = mg(\frac{1}{1 + \mu_{k}\tan\varphi})\tag{9}\]
For the given numerical values we get from (9):
\[N = 20{\cdot}9.81(\frac{1}{1 + 0.1\tan30^{\circ}})\,\textrm{N}= 196.2(\frac{1}{1 + 0.1\frac{\sqrt{3}}{3}})\,\textrm{N}\] \[N=185.5\,\textrm{N}\]
Answer: The magnitude of the normal force N (by which the sledge affects the pavement) is 185.5 N.
COMPLETE SOLUTION OF POINT 4 – The magnitude of the friction force
The magnitude of the friction force F_t is given by equation (4):
\[F_{t} = \mu_{k} N \tag{3}\]
If you substitute for N in equation (4) using equation (9), then:
\[F_{t} = mg(\frac{1}{1 + \mu_{k}\tan\varphi})\mu_{k}\tag{9}\]
For the given numerical values we get from (10):
\[F_t= 20{\cdot}9.81(\frac{1}{1 + 0.1\cdot\tan30^{\circ}})0.1\,\textrm{N}= 19.62(\frac{1}{1 + 0.1\frac{\sqrt{3}}{3}})\,\textrm{N}\] \[F_t=18.6\,\textrm{N}\]
Answer: The magnitude of the friction force F_t that affects the sledge is 18.6 N.
COMPLETE ANSWER
1) The acceleration of the sledge a equals zero.

2) The magnitude of the tension force T (by which the girl pulls the sledge) is
\[T = \frac{mg\mu_{k}}{\cos\varphi + \mu_{k}\sin\varphi}=21.4\,\textrm{N}.\]
3) The magnitude of the normal force N (by which the sledge affects the pavement) is
\[N = mg(\frac{1}{1 + \mu_{k}\tan\varphi})=185.5\,\textrm{N}.\]
4) The magnitude of the friction force F_t that affects the sledge is
\[F_{t} = mg(\frac{1}{1 + \mu_{k}\tan\varphi})\mu_{k}=18.6\,\textrm{N}.\]