A box on an inclined plane with a pulley
Task number: 510
What time does it take a box with mass m1 to go down a distance s on an inclined plane with a slope of angle α when the box is coupled by a rope and a pulley to a bucket with mass m2? The proportion m1/m2 is such that the box moves down the inclined plane. Ignore the friction force, the moment of inertia of the pulley and the mass of the rope.
Hint 1 – the motion equation
Draw a picture and mark all the forces that affect the box and the bucket. Write the motion equation for the box and the bucket.
Hint 2 – acceleration of the box
Express the acceleration of the box from the motion equations (4) and (5).
Solution to Hint 2 – acceleration of the box
We have system of two equations in two variables. From this we determine the acceleration of the system.
Adding up equations (4) and (5) yields the equation:
\[m_1g sin\alpha - m_2g=(m_1+m_2)a\]
\[a=\frac{(m_1sin\alpha - m_2)g}{m_1+m_2}\tag{6}\]
The relation (6) gives the magnitude of the acceleration with which the box moves on the inclined plane.
Hint 3 – the time it takes the box to move the distance s
Does the acceleration of the box depend on time? What kind of motion is it? How can we express the traveled distance?
COMPLETE SOLUTION
Draw a picture and mark all the forces that affect the box and the bucket. Write the motion equation for the box and the bucket.
Forces that affect the box and the bucket:
The box is affected by these forces:
\(\vec{F}_{G_1}\)…weight of the box
\(\vec{N}\)…normal force of the inclined plane
\(\vec{T}\)…tension force of the rope
The bucket is affected by these forces:
\(\vec{F}_{G_2}\)…weight of the bucket
\(\vec{T}\prime\)…tension force of the rope
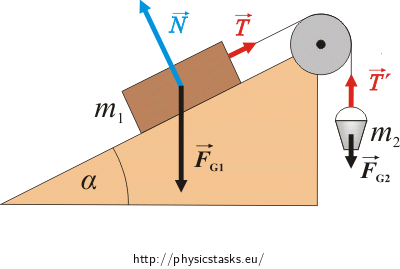
The motion equation:
The box and the bucket move with the same acceleration.
For the box:
\[\vec{F}_{G1}+\vec{N}+\vec{T}=m_1\vec{a}\]
For the bucket:
\[\vec{F}_{G2}+\vec{T}\prime=m_2\vec{a}\]
Coordinate system:
For the box:
To write the motion equation in scalar form we choose the coordinate system for the box so that the x-axis is in the direction of the motion of the box and the y-axis is orthogonal to the x-axis (see picture).
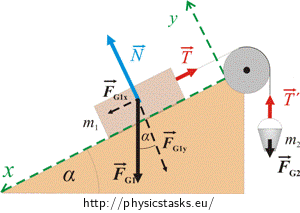
We decompose the force \(F_{G1}\) into two components in the direction of these axes:
\[F_{G1}x=F_{G1}\sin\alpha\]
\[F_{G1}y=F_{G1}\cos\alpha\]
For the bucket:
We also choose the coordinate system for the bucket so that the x-axis is in the direction of the motion of the bucket (see picture). In this case we disregard the y-axis.
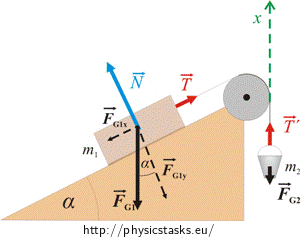
The scalar motion equation:
For the box:
\[x:\hspace{20px}F_{G1} sin\alpha - T = m_1a\tag{1}\]
\[y:\hspace{20px}N - F_{G1} cos\alpha = 0\tag{2}\]
The box isn’t moving in the direction of the y-axis and therefore the acceleration equals zero.
For the bucket:
\[x:\hspace{20px}T\prime - F_{G2} = m_2a\tag{3}\]
Because we have disregarded the mass of the pulley it has no moment of inertia and doesn’t affect the tension forces. The bucket affects the box via the rope and the box affects the bucket. According to Newton’s third law:
\[|\vec{T}|=|\vec{T}\prime|\]
We substitute \(F_{G_1}=m_1g\), \( F_{G2}=m_2g\) and rewrite equations (1) and (3):
\[m_1g sin\alpha - T = m_1a\tag{4}\]
\[T - m_2g= m_2a\tag{5}\]
We have system of two equations in two variables. From this we determine the acceleration of the system.
Adding up equations (4) and (5) yields the equation:
\[m_1g sin\alpha - m_2g=(m_1+m_2)a\]
\[a=\frac{(m_1sin\alpha - m_2)g}{m_1+m_2}\tag{6}\]
The relation (6) gives the magnitude of the acceleration with which the box moves on the inclined plane.
The time it takes the box to go down the distance s:
From equation (6) we see that the acceleration of the box does not depend on time. It is a motion with constant acceleration and it holds for the traveled distance s:
\[s=\frac{at^2}{2}\tag{7}\]
t...the time it takes the box to go down the distance s
From equation (7) we express the time t:
\[t=\sqrt{\frac{2s}{a}}\tag{8}\]
Substitute the acceleration from equation (6) into equation (8):
\[t=\sqrt{\frac{2s(m_1+m_2)}{(m_1 sin\alpha - m_2)g}}\tag{9}\]
COMPLETE ANSWER
The box goes down the distance s on the inclined plane in the time \[t=\sqrt{\frac{2s(m_1+m_2)}{(m_1 sin\alpha - m_2)g}}\] .




