A box on an inclined plane
Task number: 509
A box can be moved up an inclined plane with constant velocity by a force of magnitude F1 or down the inclined plane with constant velocity by a force of magnitude F2. Find the coefficient of kinetic friction μk between the box and the inclined plane. It holds that F1 = 6F2 and both forces are parallel with the inclined plane. The angle α between the inclined plane and the horizontal plane is 15°.
Hint 1 – forces which affect the box, the motion equation
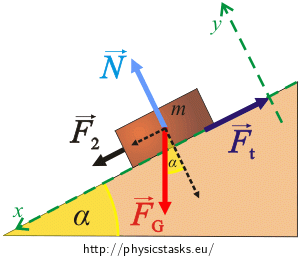
Draw a picture and mark all forces that affect the box for both situations:
1) The box is moved up by the force F1.
2) The box is moved down by the force F2.
Write the motion equation for each of these cases.
Hint 2 – friction force, determining of the coefficient of kinetic friction
Figure out what the friction force depends on and how it can be expressed. Substitute the relation for the friction force into motion equations (1) and (3). You get two equations with two variables. Express the coefficient of kinetic friction μk from these equations.
COMPLETE SOLUTION
Draw a picture and mark all forces that affect the box for both situations. Write the motion equation for each of these cases.
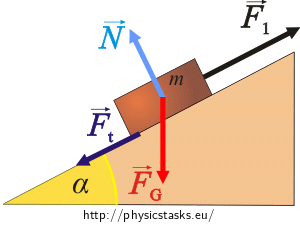
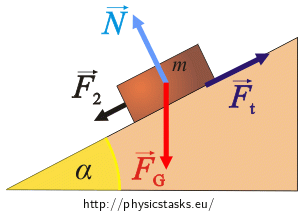
Forces that affect the box:
The box in both cases is affected by these forces:
\(\vec{F}_{G}\)…the weight of the box
\(\vec{F}_1(\vec{F}_2)\)…force pushing the box
\(\vec{N}\)…force by which the inclined plane affects the box (the normal force)
\(\vec{F}_{t}\)…friction force
The orientation of the forces is apparent from the pictures.
The box is being moved up:
The box is being moved down:
The motion equation:
The motion equation for the box that moves up the hill:
\[\vec{F}_G+\vec{N}+\vec{F}_1+\vec{F}_t=m\vec{a}_1=0\]
The motion equation for the box that moves down the hill:
\[\vec{F}_G+\vec{N}+\vec{F}_2+\vec{F}_t=m\vec{a}_2=0\]
The two motions are rectilinear with constant velocity and therefore the acceleration of the box equals zero in both cases.
The scalar motion equation:
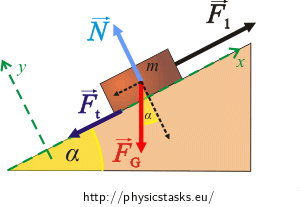
The coordinate system is chosen so that the x-axis is in the direction of the motion of the box and the y-axis is orthogonal to the x-axis.
The force FG decomposes into two components in the direction of these axes:
\[F_{Gx}=F_G\sin\alpha\]
\[F_{Gy}=F_G\cos\alpha\]
The box is moved up:
\[x:\hspace{20px}-F_G\sin\alpha+F_1-F_t=0\tag{1}\]
\[y:\hspace{20px}N-F_G\cos\alpha=0\tag{2}\]
The box is moved down:
\[x:\hspace{20px}F_G\sin\alpha+F_2-F_t=0\tag{3}\]
\[y:\hspace{20px}N-F_G\cos\alpha=0\tag{2}\]
Friction force:
The friction force that affects the box is directly proportional to the normal force by which the box affects the inclined plane. This force is, according to Newton’s third law, of the same magnitude as the force by which the inclined plane affects the box. The friction force Ft can therefore be expressed as follows:
\[F_t=\mu_k\ N\tag{4}\]
We express the force N from equation (2):
\[N=F_G\cos\alpha \]
Equation for the friction force:
\[F_t=\mu_kF_G\cos\alpha\tag{5}\]
Determining the coefficient of kinetic friction μk
We substitute into motion equations (1) and (3) the equation for the friction force (5). We express the force F1 as 6F2.
\[-F_G\sin\alpha+6F_2-F_G\mu_k\cos\alpha=0\tag{6}\]
\[F_G\sin\alpha+F_2-F_G\mu_k\cos\alpha=0 \hspace{20px}\tag{7}\]
Equation (7) is multiplied by 6 and subtracted from equation (6):
\[7F_G\sin\alpha-5F_G\mu_k\cos\alpha=0\]
\[7F_G\sin\alpha=5F_G\mu_k\cos\alpha\hspace{20px}/:(5F_G\cos\alpha)\]
\[\mu_k=\frac{7}{5}\tan\alpha\tag{8}\]
For the given numerical values we get from (8):
\[\mu_k=\frac{7}{5}\tan15^{\circ}=\frac{7}{5}\cdot0.268=0.38\]
COMPLETE ANSWER
The coefficient of kinetic friction μk between the box and the inclined plane is: \[\mu_k=\frac{7}{5}\tan\alpha=0.38\] .




