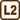Fixed Pulley
Task number: 1986
A weight with the mass of 0.55 kg and a bucket with the mass of 0.45 kg. hang on a fixed pulley. Determine the acceleration of the system and the force with which the pulley acts upon its axis. Neglect the friction and the mass of the pulley and the string.
Given values
m1 = 0.55 kg mass of the weight m2 = 0.45 kg mass of the bucket a = ? m·s−2 acceleration of the system Fk = ? N force with which the pulley acts upon its axis. Hint 1 – Equations of motion, calculation of acceleration
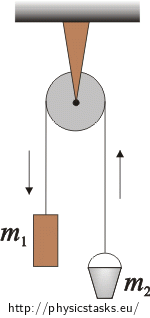
Draw a free body diagram and mark all the forces acting upon the weight and the bucket into the diagram. Write the equations of motion for the bucket and the weight. Choose a coordinate system.
Hint 2 – Force acting upon the axis of the pulley
The force with which the pulley acts upon its axis is, according to Newton's third law, equal to the force with which the axis acts upon the pulley. Draw all the forces acting upon the pulley and realise what the net force is.
OVERALL SOLUTION
Forces acting upon the weights:
Weight m1:
\(\vec{F}_\mathrm{G1}\)…gravitational force
\(\vec{T}_1\)…tensile force of the string
Bucket m2:
\(\vec{F}_\mathrm{G2}\)…gravitational force
\(\vec{T}_2\)…tensile force of the string
Equations of motion:
Weight m1:
\[\vec{F}_\mathrm{G1}+\vec{T}_1\,=\,m_1\vec{a}.\]Bucket m2:
\[\vec{F}_\mathrm{G2}+\vec{T}_2\,=\,m_2\vec{a}.\]The weight and the bucket move with the same acceleration in opposite directions.
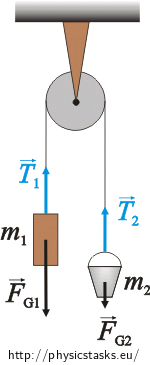
We choose the y axis as depicted in the picture. We rewrite the equations using scalars:
\[F_\mathrm{G1} - T_1 \,=\, m_1a,\tag{1}\] \[T_2 - F_\mathrm{G2} \,=\, m_2a.\tag{2}\]Because we neglect the mass of the pulley, it has no moment of inertia and does not affect the forces of the string. The weight m1 acts upon the bucket m2 through the string and vice versa. According to Newton's third law of motion, it holds for the magnitudes of the string forces that:
\[|\vec{T}_1| \,=\, |\vec{T}_2| \,=\, |\vec{T}|\,.\]We substitute into equations (1) and (2):
\[m_1g - T \,=\, m_1a,\tag{3}\] \[T - m_2g \,=\, m_2a.\tag{4}\]Calculation of acceleration:
By adding equations (3) and (4) we obtain:
\[m_1g - m_2g \,=\, m_1a+m_2a,\] \[(m_1 - m_2)g \,=\, (m_1+m_2)a,\] \[a\,=\,\frac{(m_1 - m_2)g}{m_1+m_2}.\tag{5}\]We substitute numerically and calculate the acceleration:
\[a\,=\,\left(\frac{\left(0.55\,-\,0.45\right)9.81}{0.55+0.45}\right)\,\mathrm{m\cdot s^{-2}}\,\dot=\,0.98\,\mathrm{m\cdot s^{-2}}\,.\]Tensile forces \(\vec{T}_1^\prime\) and \(\vec{T}_2^\prime\) act on both sides of the pulley. Also the force \(\vec{F}_\mathrm{p}\) with which the axis is fixed in place acts upon the pulley (we neglect the mass of the pulley and therefore the gravitational force acting upon it).
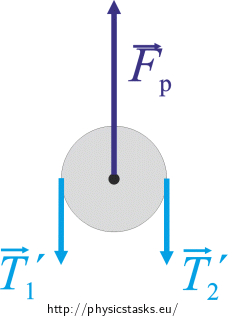
The translational acceleration is zero, so the resultant of the forces acting upon it is also zero:
\[\vec{T}_1^\prime\,+\,\vec{T}_2^\prime\,+\,\vec{F}_\mathrm{p}\,=\,0\,.\tag{6}\]Because we neglect the mass of the pulley, it has no moment of inertia and does not affect the string forces. According to Newton's third law of motion, it holds for the string forces that:
\[|\vec{T}_1^\prime| \,=\, |\vec{T}_2^\prime| \,=\, |\vec{T}|\,.\]We rewrite equation (6) using scalars:
\[2T\,-\,F_\mathrm{p}\,=\,0,\] \[2T\,=\,F_\mathrm{p}.\tag{7}\]We can express the tensile force from equation (3) or (4):
\[F_\mathrm{p}\,=\,2m_2\left(a+g\right)\,=\,2m_1\left(g-a\right)\,.\tag{8}\]We substitute numerically into equation (8):
\[F_\mathrm{p}\,=\,2\,\cdot\,0.45\left(9.81\,+\,0.98\right)\,\mathrm{N}\,=\,2\,\cdot\,0.55\left(9.81\,-\,0.98\right)\,\mathrm{N},\] \[F_\mathrm{p}\,=\,0.9\,\cdot10.79\,\mathrm{N}\,=\,1.1\,\cdot8.83\,\mathrm{N},\] \[F_\mathrm{p}\,\dot=\,9.71\,\mathrm{N}.\]ANSWER
The acceleration of the system is \(a\,\dot=\,0.98\,\mathrm{m\cdot s^{-2}}\).
The force with which the pulley acts upon its axis is \(F_\mathrm{p}\,\dot=\,9.71\,\mathrm{N}\).