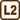A pulley system
Task number: 508
A bucket with mass m2 and a block with mass m1 are hung on a pulley system. Find the magnitude of the acceleration with which the bucket and the block are moving and the magnitude of the tension force T by which the rope is stressed. Ignore the masses of the pulley system and the rope. The bucket moves up and the block moves down.
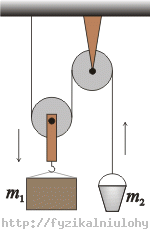
Hint 1 – the forces in the pulley system and the force equations
Figure out which forces affect the bucket and the block. Draw a picture. Write down the force equations for the bucket and the block.
Hint 2 – the scalar force equations, tension forces
Choose a suitable coordinate system and rewrite the force equations to scalar form. Decide what relations will hold for the magnitude of the tension forces T, T' and T''.
Hint 3 – acceleration
Decide what the magnitude of the acceleration a1 will be in relation to a2. Imagine that the bucket goes up a distance s what distance does the block go down?
Hint 4 – the magnitude of the acceleration, the force T
We have two equations (8) and (9) in two variables T and a1. Solve these equations and from equation (7) determine the magnitude of the acceleration a2.
COMPLETE SOLUTION
Draw all the forces which affect the bucket and the block in the picture. Write the force equations for them.
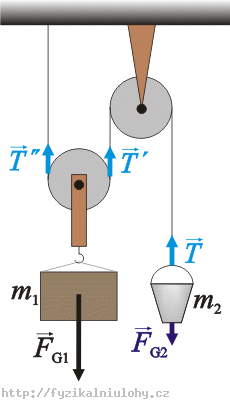
Forces that affect the bucket m2:
\(\vec{F}_{G_2}\)…weight
\(\vec{T}\)…tension force by which the rope affects the bucket
Forces that affect the block m1:
\(\vec{F}_{G_1}\)…weight
\(\vec{T}\prime\)…tension force by which the rope affects the block
\(\vec{T}\prime\prime\)…tension force by which the rope affects the block
The vector force equation for the bucket:
\[\vec{F}_{G2}+\vec{T}=m_2\vec{a}_2\tag{1}\]
The vector force equation for the block:
\[\vec{F}_{G1}+\vec{T}\prime+\vec{T}\prime\prime=m_1\vec{a_1}\tag{2}\]
We choose the y-axis the way it is marked on the picture.
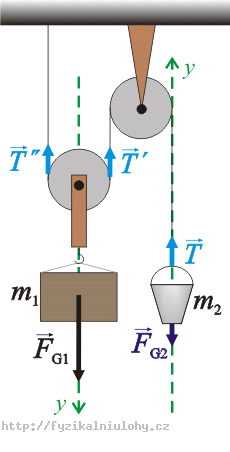
We rewrite equations (1) and (2) to scalar form:
\[T-F_{G2}= m_2a_2\tag{3}\]
\[F_{G1}-T\prime-T\prime\prime = m_1a_1\tag{4}\]
Because we leave the mass of the pulley system and the rope out of account they have no moment of inertia and don’t affect the tension forces. The following holds for the magnitude of the tension forces:
\[|\vec{T}|=|\vec{T}\prime|=|\vec{T}\prime\prime|\]
We rewrite equations (3) and (4):
\[T-F_{G2}= m_2a_2\tag{5}\]
\[F_{G1}-2T= m_1a_1\tag{6}\]
Relation between the magnitudes of acceleration a1 and a2:
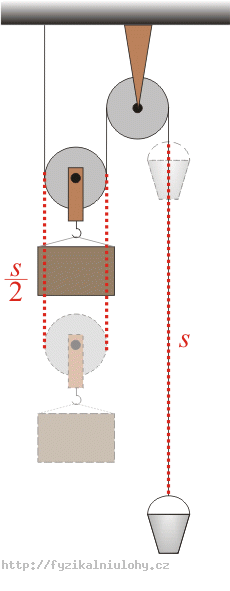
If the bucket goes up a distance s, the block goes down a distance \(\frac{s}{2}\).
\[s=\frac{1}{2}a_2t^2\]
\[\frac{s}{2}=\frac{1}{2}a_1t^2\]
We divide the first equation by the second equation, yielding:
\[2=\frac{a_2}{a_1}\]
\[a_2=2a_1\tag{7}\]
Equation (5) and equation (6) can be written as:
\[T-m_2g= m_22a_1\tag{8}\]
\[m_1g-2T= m_1a_1\tag{9}\]
We have two equations (8) and (9) in two variables T and a1. From them we can determine the magnitude of the acceleration a1 and the force T. We multiply equation (8) by 2 and add both equations up:
\[m_1g-2m_2g= m_1a_1+4m_2a_1\]
\[(m_1-2m_2)g= (m_1+4m_2)a_1\]
\[a_1=\frac{(m_1-2m_2)g}{m_1+4m_2}\tag{10}\]
According to equation (7):
\[a_2=2a_1=2\frac{(m_1-2m_2)g}{m_1+4m_2}=\frac{(2m_1-4m_2)g}{m_1+4m_2}\tag{11}\]
The magnitude of the tension force T is given for example by equation (8):
\[T-m_{2g}= m_22a_1\]
\[T=m_22a_1+m_{2g}=m_2\frac{2(m_1-2m_2)g}{m_1+4m_2}+m_2g\]
\[T=\frac{2(m_2m_1-2m_2^2)g}{m_1+4m_2}+m_2g =\frac{(2m_2m_1-4m_2^2+m_2(m_1+4m_2))g}{m_1+4m_2}\]
\[T=\frac{(2m_2m_1-4m_2^2+m_2m_1+4m_2^2)g}{m_1+4m_2}= \frac{3m_2m_1g}{m_1+4m_2}\]
\[T=\frac{3m_2m_1g}{m_1+4m_2}\tag{12}\]
COMPLETE ANSWER
The magnitude of the acceleration with which the block moves is \(a_1=\frac{(m_1-2m_2)g}{m_1+4m_2}\).
The magnitude of the acceleration with which the bucket moves is \(a_2=2a_1=\frac{(2m_1-4m_2)g}{m_1+4m_2}\).
The magnitude of the tension force T which affects the rope is \(T=\frac{3m_2m_1g}{m_1+4m_2}\).